Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
Невдовзі після старту кінетична енергія ракети дорівнювала $E$. Через деякий час польоту її швидкість збільшилася в 3 рази, а маса зменшилася в 3 рази. Визначте, якою стала кінетична енергія ракети.
Б
$3 E$
Правильна відповідь
М'яч до зіткнення зі стінкою мав імпульс величиною $p_{0}$. Після зіткнення зі стінкою величина імпульсу м'яча становить $p_{0} / 2$. Кінетична енергія м’яча внаслідок зіткнення зі стінкою
Б
зменшилася вчетверо
Правильна відповідь
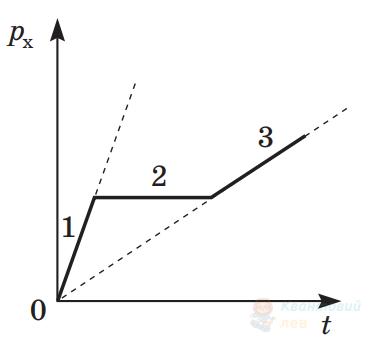
За графіком залежності проекції імпульсу $p_{\mathrm{x}}$ тіла від часу $t$ укажіть правильне співвідношення між проекціями на вісь $O x$ рівнодійних $F_{1}, F_{2}, F_{3}$ сил, що діють на тіло відповідно протягом інтервалів часу $1,2,3$.
Б
$F_{1}>F_{3} ; F_{2}=0$
Правильна відповідь
Кулька, що рухалася зліва направо зі швидкістю $10 \mathrm{~м} / \mathrm{с}$, зіткнулася з такою самою нерухомою кулькою. На рисунках наведено можливі напрямки та модулі швидкості руху кульок після зіткнення. Який з рисунків відповідає результату пружного зіткнення?
Г
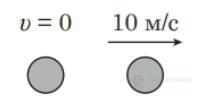 Правильна відповідь
Правильна відповідь
Укажіть фізичну величину, одиницю якої визначають через основні одиниці Міжнародної системи одиниць (SI) як $\frac{\mathrm{кг} \cdot \mathrm{м}^{2}}{\mathrm{с}^{3}}$.
Б
потужність
Правильна відповідь
Швидкість криголама масою $1000 \mathrm{~т}$, який рівномірно рухався з вимкненим двигуном, становила $6 \mathrm{~м} / \mathrm{с}$. Після зіткнення з нерухомою крижиною криголам продовжив рівномірний прямолінійний рух разом із нею. Маса крижини становить $5 \cdot 10^{5} \mathrm{~кг}$. Яка швидкість сумісного руху обох тіл? Тертям між водою і криголамом знехтуйте. Уважайте, що вода стояча, течій немає.
А
$4 \mathrm{~м} / \mathrm{с}$
Правильна відповідь
Б
$3 \mathrm{~м} / \mathrm{с}$
В
$0,4 \mathrm{~м} / \mathrm{с}$
Г
$0,04 \mathrm{~м} / \mathrm{с}$
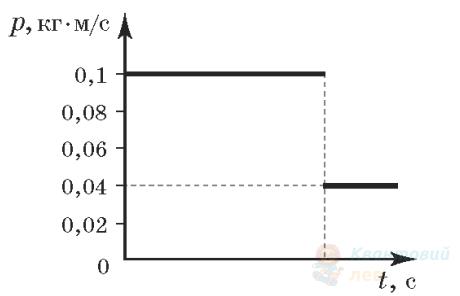
Порожній вагон іграшкової залізничної дороги, рухаючись по горизонтальній колії, стикається з нерухомим навантаженим вагоном і зчіплюється з ним. За графіком залежності імпульсу порожнього вагона від часу визначте масу вантажу в другому вагоні. Маса кожного порожнього вагона дорівнює $1 \mathrm{~кг}$.
В
$500 \mathrm{~г}$
Правильна відповідь
Тепловоз масою $M$, який рухався зі швидкістю $v$, зчіплюється з вагоном масою $m$, що рухається в тому самому напрямку зі швидкістю $u$. Якою буде їхня швидкість руху відразу після зчеплення?
А
$\frac{(M+m) \cdot (M v+m u)}{M \cdot m}$
Б
$\frac{M \cdot (v+u)}{m}$
В
$\frac{m \cdot (v+u)}{M}$
Г
$\frac{M v+m u}{M+m}$
Правильна відповідь
Дві кулі з однаковими масами $m_{1}=m_{2}=m$ рухались назустріч одна одній з однаковими за модулем швидкостями $v_{1}=v_{2}=v$. Після непружного зіткнення обидві кулі зупинились. Чому дорівнює зміна загального імпульсу системи цих двох тіл унаслідок зіткнення?
Автомобіль масою $1 \mathrm{~т}$ рухається рівномірно по мосту на висоті $5 \mathrm{~м}$ над поверхнею землі. Швидкість автомобіля дорівнює $10 \mathrm{~м} / \mathrm{с}$. Визначте імпульс і кінетичну енергію автомобіля.
А
$10^{4} \mathrm{кг} \cdot \mathrm{~м} / \mathrm{с}$;
$10^{5} \mathrm{~Дж}$
Б
$10^{4} \mathrm{кг} \cdot \mathrm{~м} / \mathrm{с}$;
$5 \cdot 10^{4} \mathrm{~Дж}$
Правильна відповідь
В
$ 5 \cdot 10^{4} \mathrm{кг} \cdot \mathrm{~м} / \mathrm{с}$;
$10^{4} \mathrm{~Дж}$
Г
$10^{5} \mathrm{кг} \cdot \mathrm{~м} / \mathrm{с}$;
$10^{4} \mathrm{~Дж}$
Швидкість тіла масою $0,8 \mathrm{~кг}$, що рухається вздовж осі $O X$, змінюється відповідно до рівняння $v_{x}=0,05 \sin (10 \pi t)$, де всі величини виражено в одиницях SI. Визначте імпульс тіла через $0,2 \mathrm{~c}$ після початку відліку часу.
А
$0 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
Правильна відповідь
Б
$0,001 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
В
$0,002 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
Г
$0,04 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
На залізничній вантажній платформі масою $20 \mathrm{~т}$, що перебуває в стані спокою, стоїть слон масою $5 \mathrm{~т}$. Він починає рухатися платформою вздовж колії зі швидкістю $2 \mathrm{~м}/\mathrm{с}$ відносно платформи. Силу тертя між колесами платформи та колією не враховуйте.
Визначте швидкість руху платформи відносно землі.
Відповідь запишіть у метрах на секунду ($\mathrm{м} / \mathrm{с}$).
Під час комплектування потяга другий вагон масою $45 \mathrm{~т}$ наздоганяє перший вагон масою $55 \mathrm{~т}$, що рухався поперед нього в тому ж напрямку зі швидкістю $3 \mathrm{~м} / \mathrm{с}$. Після зіткнення вагони зчіплюються і продовжують рухатися зі швидкістю $3,9 \mathrm{~м} / \mathrm{с}$.
Визначте швидкість руху другого вагона до зіткнення з першим вагоном.
Відповідь запишіть у метрах за секунду ($\mathrm{м} / \mathrm{с}$).
Куля масою $400 \mathrm{~г}$, рухаючись горизонтальною поверхнею зі швидкістю $5 \mathrm{~м}/\mathrm{с}$, наздоганяє іншу кулю масою $200 \mathrm{~г}$, що рухається зі швидкістю $2 \mathrm{~м}/\mathrm{с}$. Удар непружний, центральний.
Визначте швидкість руху куль після удару.
Відповідь запишіть у метрах на секунду ($\mathrm{м} / \mathrm{с}$)
Куля масою $400 \mathrm{~г}$, рухаючись горизонтальною поверхнею зі швидкістю $5 \mathrm{~м}/\mathrm{с}$, наздоганяє іншу кулю масою $200 \mathrm{~г}$, що рухається зі швидкістю $2 \mathrm{~м}/\mathrm{с}$. Удар непружний, центральний.
Визначте втрати кінетичної енергії внаслідок удару.
Відповідь запишіть у джоулях ($\mathrm{Дж}$)
Пластилінова кулька масою $100 \mathrm{~г}$, що рухалася зі швидкістю $2,2 \mathrm{~м}/\mathrm{с}$, зазнала абсолютно непружного зіткнення з нерухомою кулькою масою $10 \mathrm{~г}$. Визначте, на скільки зменшилася механічна енергія кульок унаслідок зіткнення. Відповідь запишіть у міліджоулях.
Правильна відповідь:
22.0
Школяр масою $50 \mathrm{~кг}$, стоячи на гладенькому льоду, кидає ядро масою $5 \mathrm{~кг}$ під кутом $60^{\circ}$ до горизонту зі швидкістю $8 \mathrm{~м}/\mathrm{с}$. Якої швидкості набуває школяр? Відповідь запишіть у $\mathrm{м}/\mathrm{с}$.
Початкова швидкість снаряду, випущеного з гармати вертикально вгору, дорівнює $40 \mathrm{~м} / \mathrm{с}$. У точці максимального підйому снаряд розірвався на два осколки, маси яких відносяться як $1: 5$. Осколок меншої маси полетів горизонтально зі швидкістю $20 \mathrm{~м} / \mathrm{с}$. На якій відстані (у метрах) від точки пострілу впаде осколок більшої маси? Вважайте поверхню Землі плоскою та горизонтальною; $g=10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Правильна відповідь:
16.0
Вагон масою $50 \mathrm{~т}$ наздоганяє порожній вагон масою $25 \mathrm{~т}$, що рухається зі швидкістю $2 \mathrm{~м} / \mathrm{с}$. Після зчеплення вагони рухаються зі швидкістю $3 \mathrm{~м} / \mathrm{с}$. Рух вагонів уважайте прямолінійним, а рейки – паралельними.
Визначте, із якою швидкістю ($\mathrm{м} / \mathrm{с}$) рухався перший вагон до зіткнення.
Вагон масою $50 \mathrm{~т}$ наздоганяє порожній вагон масою $25 \mathrm{~т}$, що рухається зі швидкістю $2 \mathrm{~м} / \mathrm{с}$. Після зчеплення вагони рухаються зі швидкістю $3 \mathrm{~м} / \mathrm{с}$. Рух вагонів уважайте прямолінійним, а рейки – паралельними.
Визначте, яка частка (%) механічної енергії двох вагонів перетворилася у внутрішню енергію внаслідок непружной взаємодії.
Два тіла масами $2 \mathrm{~кг}$ і $3 \mathrm{~кг}$, що рухалися у взаємно перпендикулярних напрямках один до одного зі швидкостями $3$ і $2 \mathrm{~м}/\mathrm{с}$ відповідно, злиплися при зіткненні. Яка кількість тепла виділилася при цьому?
Відповідь запишіть у джоулях.
На залізничній вантажній платформі масою $20 \mathrm{~т}$, що перебуває в стані спокою, стоїть слон масою $5 \mathrm{~т}$. Він починає рухатися платформою вздовж колії зі швидкістю $2 \mathrm{~м}/\mathrm{с}$ відносно платформи. Силу тертя між колесами платформи та колією не враховуйте.
Обчисліть кінетичну енергію платформи відносно землі.
Відповідь запишіть у кілоджоулях ($\mathrm{кДж}$).
Тіло, маса якого дорівнює $990 \mathrm{~г}$, лежить на горизонтальній поверхні. У тіло влучає куля масою $10 \mathrm{~г}$ і застрягає в ньому. Швидкість кулі дорівнює $600 \mathrm{~м}/\mathrm{с}$ і напрямлена горизонтально. Визначте, з якою швидкістю почне рухатися тіло після попадання в нього кулі. Тертям між тілом і поверхнею можна знехтувати.
Тіло, маса якого дорівнює $990 \mathrm{~г}$, лежить на горизонтальній поверхні. У нього влучає куля масою $10 \mathrm{~г}$ і застрягає в ньому. Швидкість кулі напрямлена горизонтально. Визначте початкову швидкість кулі, якщо після її влучання в тіло, воно починає рухатися зі швидкістю $6 \mathrm{~м}/\mathrm{с}$. Тертям між тілом і поверхнею можна знехтувати.
Правильна відповідь:
600.0
Під час вільного падіння імпульс м’яча збільшився на $12 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$ за $2$ секунди. Обчисліть масу м'яча. Вважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Відповідь запишіть у кілограмах ($\mathrm{кг}$).