Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
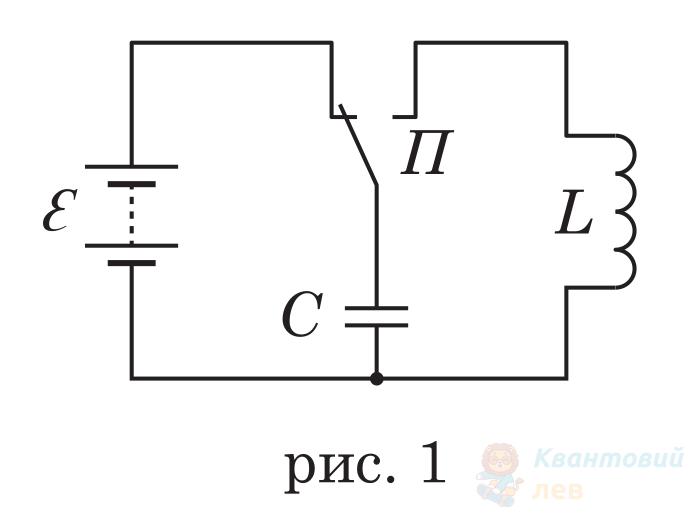
Для намагнічування залізних предметів зібрали електричне коло за схемою (див. рисунок 1). Конденсатор $C$ спочатку зарядили від джерела постійного струму $\varepsilon$, а потім перемикачем $П$ приєднали до котушки індуктивності $L$. Усередині котушки розміщено предмет, який збиралися намагнітити. Проте виявилося, що установка працювала погано: предмети намагнічувалися дуже слабко, і неможливо передбачити, як будуть розташовані на них магнітні полюси.
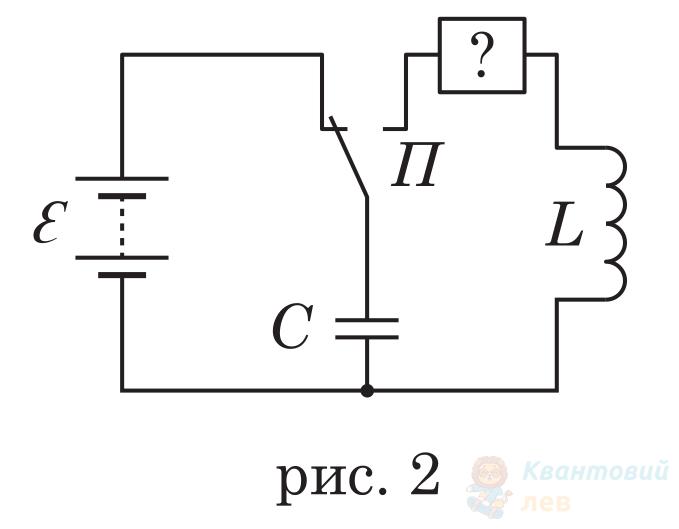
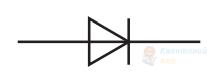
Визначте, який з елементів (А – Г) потрібно добавити в коло (див. рисунок 2), щоб посилити намагнічування.
А
 Правильна відповідь
Правильна відповідь
У скільки разів збільшується енергія магнітного поля котушки індуктивності, якщо сила струму в ній зростає в 3 рази?
В
у 9 разів
Правильна відповідь
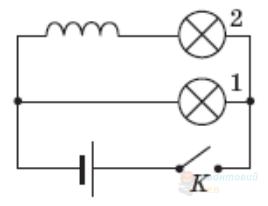
У схемі електричного кола, зображеній на рисунку, лампочки 1 і 2 є однаковими. Під час замикання ключа $К$ лампочка 2 загорається на $0,5 \mathrm{~c}$ пізніше, ніж лампочка 1 , тому що
А
дріт, з якого виготовлено котушку, має досить великий опір.
Б
лампочка 2 знаходиться далі від джерела електрорушійної сили, ніж лампочка 1.
В
у котушці виникає електрорушійна сила самоіндукції, що перешкоджає зростанню струму в ній.
Правильна відповідь
Г
електрони сповільнюються на ділянках кола, що вигинаються.
Укажіть правильний запис одиниці індуктивності провідника, вираженої через основні одиниці SI.
А
$\frac { \mathrm{кг} \cdot \mathrm{м}^{2}} {\mathrm{А} \cdot \mathrm{с}^{2} }$
Правильна відповідь
Б
$\frac { \mathrm{кг} \cdot \mathrm{м}^{2}} {\mathrm{А} \cdot \mathrm{с}^{2} }$
В
$\frac { \mathrm{кг} \cdot \mathrm{м}} {\mathrm{А} \cdot \mathrm{с}^{2} }$
Г
$\frac { \mathrm{кг} \cdot \mathrm{м}^{2}} {\mathrm{А} \cdot \mathrm{с}^{3} }$
Після розмикання кола живлення котушки з індуктивністю $2 \mathrm{~Гн}$ на клемах вимикача виникала ЕРС самоіндукції $300 \mathrm{~В}$. Сила струму до розмикання кола становила $1,5 \mathrm{~А}$. Вважаючи, що сила струму в колі змінювалась рівномірно, визначте час існування струму в котушці після розмикання кола.
А
$10 \mathrm{~мс}$
Правильна відповідь
Правильно продовжте твердження: під час незатухаючих електромагнітних коливань, у момент, коли конденсатор має максимальний заряд, максимального значення досягає ...
А
Повна енергія електромагнітних коливань
В
Енергія електричного поля
Правильна відповідь
Індуктивність котушки коливального контура дорівнює $20 \mathrm{~мГн}$. Визначте ємність конденсатора, якщо максимальна напруга на ньому становить $80 \mathrm{~В}$, а максимальна сила струму в котушці дорівнює $2 \mathrm{~А}$. Коливання в контурі вважайте незатухаючими.
В
$12,5 \mathrm{~мкФ}$
Правильна відповідь
Заряджений конденсатор ємністю $C$ з'єднали з котушкою, індуктивність якої дорівнює $L$. Визначте, через який час уся енергія електричного поля конденсатора перетвориться в енергію магнітного поля котушки. Активним опором елементів кола можна знехтувати.
А
$\frac{\pi}{4} \sqrt{L C}$
Б
$\frac{\pi}{2} \sqrt{L C}$
Правильна відповідь
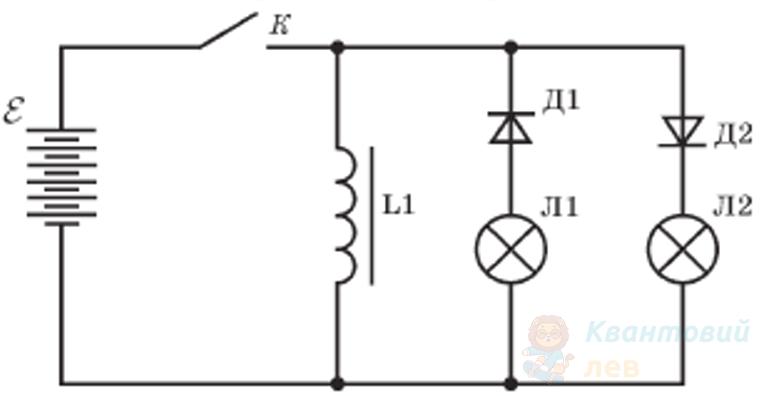
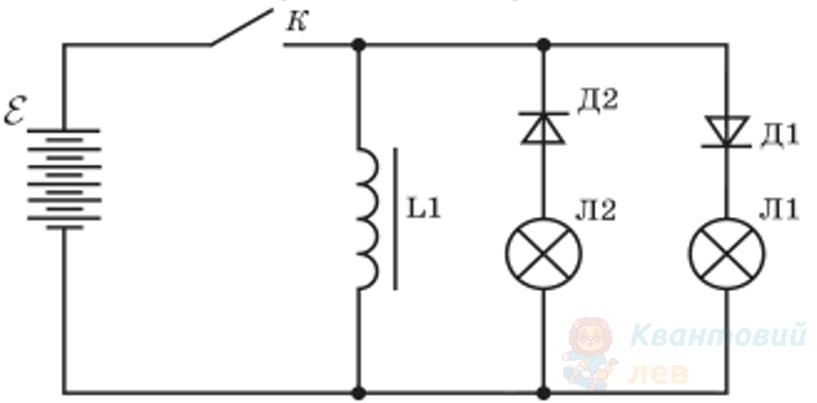
Визначте, які лампочки спалахуватимуть при періодичному замиканні та розмиканні вимикача, якщо індуктивність котушки L1 досить велика.
А
Доки вимикач замкнутий, горить обидві лампочки, при розмиканні обидві гаснуть.
Б
Доки вимикач замкнутий, горить Л2, при розмиканні спалахує Л1.
Правильна відповідь
В
Доки вимикач замкнутий, горить Л1, при розмиканні спалахує Л2.
Г
При замиканні спалахує Л1, при розмиканні спалахує Л2.
Визначте, які лампочки спалахуватимуть при періодичному замиканні та розмиканні вимикача, якщо індуктивність котушки L1 досить велика.
А
Доки вимикач замкнутий, горить обидві лампочки, при розмиканні обидві гаснуть.
Б
Доки вимикач замкнутий, горить Л2, при розмиканні спалахує Л1.
В
Доки вимикач замкнутий, горить Л1, при розмиканні спалахує Л2.
Правильна відповідь
Г
При замиканні спалахує Л2, при розмиканні спалахує Л1.
Установіть відповідність між назвою одиниці фізичної величини та її виразом в основних одиницях SI.
Варіанти справа
А
$\frac{\mathrm{кг} \cdot \mathrm{м}^{2}}{\mathrm{с}^{2} \cdot \mathrm{~A}^{2}}$
Б
$\frac{\mathrm{кг} \cdot \mathrm{м}^{2}}{\mathrm{с}^{2}}$
В
$\frac{\mathrm{кг}}{\mathrm{с}^{2} \cdot \mathrm{~A}}$
Г
$\frac{\mathrm{кг} \cdot \mathrm{м}^{2}}{\mathrm{с}^{2} \cdot \mathrm{~A}}$
Д
$\frac{\mathrm{кг} \cdot \mathrm{м}}{\mathrm{с}^{2}}$
Установіть відповідність між фізичними величинами та їхніми математичними виразами.
Варіанти зліва
1
електрорушійна сила самоіндукції
Варіанти справа
Г
$\frac{-L \Delta I}{\Delta t}$
До котушки індуктивності під’єднали заряджений конденсатор. У колі виникли електромагнітні коливання. Індуктивність котушки $10 \mathrm{~мГн}$, ємність конденсатора $40 \mathrm{~мФ}$. Активним опором кола знехтуйте.
Через який найменший час після з'єднання енергія магнітного поля котушки зрівняється з енергією електричного поля конденсатора? Уважайте, що $\pi=3,14$.
Відповідь запишіть у мілісекундах ($\mathrm{мс}$) й округлять до одиниць
Правильна відповідь:
16.0
Котушку індуктивністю $2 \mathrm{~Гн}$ підключили до акумулятора. За час зростання сили струму до $5 \mathrm{~А}$ у колі виділилася кількість теплоти $70 \mathrm{~Дж}$. Визначте роботу джерела струму за цей час. Утратами енергії на електромагнітне випромінювання знехтуйте. Відповідь запишіть у джоулях.
Правильна відповідь:
95.0
Котушка індуктивністю $50 \mathrm{~мкГн}$ послідовно приєднана до конденсатора. Визначте ємність конденсатора, якщо контур резонує на довжину хвилі $600 \mathrm{~м}$. Уважайте, що $\pi^{2}=10$.
Відповідь запишіть у нанофарадах.
У котушці за 1 хвилину сила струму збільшується від $10 \mathrm{~А}$ до $130 \mathrm{~А}$. Обчисліть індуктивність ($\mathrm{Гн}$) котушки, якщо ЕРС (електрорушійна сила) самоіндукції дорівнює $50 \mathrm{~В}$.
Правильна відповідь:
25.0
Струм силою $20 \mathrm{~А}$, пропущений крізь обмотку котушки, створює в ній магнітний потік $0,5 \mathrm{~Вб}$. Обчисліть енергію магнітного поля цієї котушки.
Відповідь запишіть у джоулях.
Визначте енергію магнітного поля котушки, що має індуктивність $3 \mathrm{~Гн}$, по якій проходить струм силою $0,5 \mathrm{~A}$.
Відповідь запишіть у джоулях.
Правильна відповідь:
0.375
У котушці, індуктивність якої дорівнює $0,8 \mathrm{~Гн}$, при рівномірному зростанні сили струму виникла електрорушійна сила самоіндукції, модуль якої дорівнює $1,2 \mathrm{~В}$. На скільки збільшується сила струму за 1 секунду?
Відповідь запишіть в амперах.
Визначте індуктивність котушки, якщо відомо, що по ній протікає струм $20 \mathrm{~А}$, а енергія магнітного поля котушки становить $100 \mathrm{~Дж}$. Відповідь подайте в генрі.
Визначте магнітний потік (у $\mathrm{Вб}$), що виникає в соленоїді, індуктивність якого дорівнює $0,05 \mathrm{~Гн}$, сила струму у витках дорівнює $2 \mathrm{~А}$.
Визначте силу струму (в амперах) у соленоїді індуктивністю $0,05 \mathrm{~Гн}$, якщо в ньому виникає магнітний потік $0,1 \mathrm{~Вб}$.