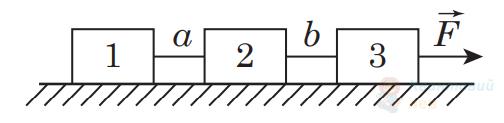Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
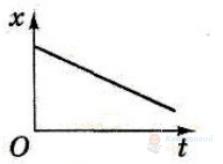
Декілька тіл рухаються вздовж осі Ох інерціальної системи відліку. Укажіть графік, який відповідає руху за інерцією.
А
 Правильна відповідь
Правильна відповідь
Пов’язану із Землею систему відліку можна вважати інерціальною. Виберіть з-поміж наведених тіл те, з яким можна пов’язати початок координат інерціальної системи відліку.
А
автомобіль, що розганяється
Б
поїзд, що виконує поворот
В
яблуко, що вільно падає на землю
Г
шайба, що без тертя прямолінійно ковзає по льоду
Правильна відповідь
Яка з характеристик руху обов'язково лишається незмінною під час переходу від однієї інерціальної системи відліку до іншої?
Б
прискорення
Правильна відповідь
Узгодьте закон (1-4) із прикладом (А – Д), що йому відповідає.
Варіанти зліва
4
закон всесвітнього тяжіння
Варіанти справа
А
зменшення маси гоночного автомобіля (двигун залишився той самий) привело до швидшого розгону
Б
унаслідок різкого гальмування гальмівні колодки автомобіля нагріваються
В
кинутий вертикально вгору камінь упав на поверхню землі
Г
якщо сила тертя компенсує силу тяжіння, то дощова крапля падає на землю рівномірно прямолінійно
Д
сила удару, якого завдав комар, улетівши в лобове скло рухомого автомобіля, дорівнює силі удару, якого завдало лобове скло комару
Установіть відповідність між напрямком рівнодійної $\vec{F}$ усіх діючих на тіло сил (1-4) і прикладом руху (А-Д), де $\vec{v}$ – швидкість руху тіла.
Варіанти зліва
1
напрямки $\vec{F}$ і $\vec{v}$ збігаються
2
напрямок $\vec{F}$ протилежний напрямку $\vec{v}$
3
напрямки $\vec{F}$ і $\vec{v}$ утворюють прямий кут
4
напрямки $\vec{F}$ і $\vec{v}$ утворюють гострий кут
Варіанти справа
А
автобус гальмує перед зупинкою, рухаючись прямолінійно
Б
футбольний м'яч піднімається, спрямований воротарем на іншу половину футбольного поля
В
снаряд рухається всередині ствола гармати при пострілі
Г
електрон рухається в магнітному полі під кутом до ліній магнітної індукції
Д
камінець, який кинули під кутом до горизонту, опускається
Установіть відповідність між силою (1-4), що діє на тіло, та характером руху тіла (А – Д).
Варіанти зліва
1
сила весь час перпендикулярна до швидкості
2
сила зберігає напрямок і величину незмінними
3
напрямок сили збігається з напрямком швидкості
4
напрямок сили протилежний напрямку швидкості
Варіанти справа
Б
рух прямолінійний рівномірний
В
рух криволінійний рівномірний
Г
модуль швидкості зменшується
Д
рух з постійним прискоренням
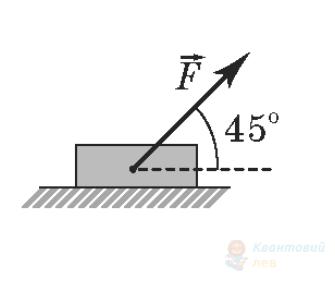
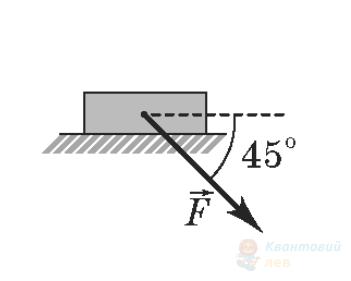
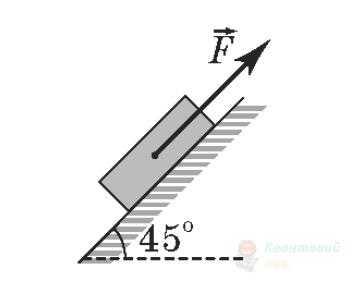
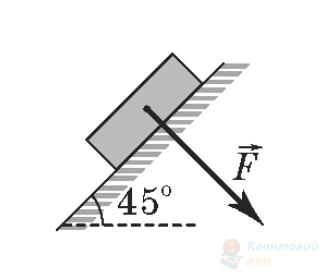
До тіла масою $m$ прикладено силу $F$, як зображено на рисунках. Установіть відповідність між рисунком і виразом для модуля сили реакції опори. Вважайте, що в усіх випадках для модулів сил виконується співвідношення $mg > \sqrt{2} F$.
Варіанти справа
А
$\frac{\sqrt{2}}{2} m g – F$
Б
$\frac{\sqrt{2}}{2} m g + F$
Г
$m g – \frac{\sqrt{2}}{2} F$
Д
$m g + \frac{\sqrt{2}}{2} F$
Установіть відповідність між фізичним законом та формулою, що його описує:
Варіанти зліва
1
закон збереження імпульсу;
2
другий закон динаміки Ньютона;
3
третій закон динаміки Ньютона;
4
закон всесвітнього тяжіння.
Варіанти справа
А
$F=G \frac{m_{1} m_{2}}{r^{2}}$
Б
$\vec{F}_{12}=-{\vec{F}}_{21}$
Г
$m_{1} \vec{\nu}_{1}+m_{2} \vec{\nu}_{2}=m_{1} \vec{u}_{1}+m_{2} \vec{u}_{2}$
Д
$\vec{a}=\frac{\vec{F}}{m}$
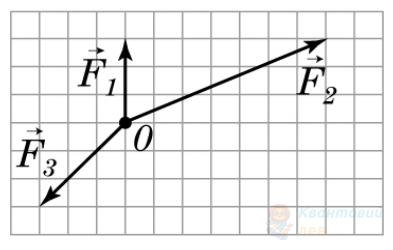
До центра мас тіла (точка $O$), що лежить на горизонтальній поверхні, прикладено три сили так, як показано на рисунку. Визначте модуль прискорення, якого набуде тіло під дією цих сил. Маса тіла дорівнює $2 \mathrm{~кг}$. Уважайте, що вектори сил зображено на рисунку в масштабі, за якого розміри сторони клітинки відповідають модулю сили $1 \mathrm{~Н}$.
Відповідь запишіть у метрах за секунду у квадраті ($\mathrm{м} / \mathrm{с}^{2}$).
Вантаж масою $100 \mathrm{~кг}$ тягнуть уздовж горизонтальної поверхні за допомогою мотузки, паралельної площині цієї поверхні. За рівномірного руху вантажу сила натягу, що виникає в мотузці, дорівнює $20 \mathrm{~Н}$. Визначте мінімальний час переміщення цього вантажу зі стану спокою на відстань $5 \mathrm{~м}$, якщо мотузка може витримати максимальну силу натягу $30 \mathrm{~Н}$.
Відповідь запишіть у секундах ($\mathrm{с}$).
Правильна відповідь:
10.0
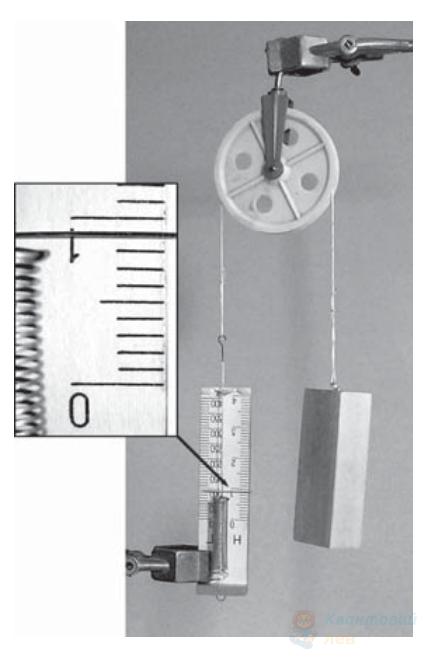
Визначте масу бруска, що висить на нитці (див. рисунок). Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у грамах ($\mathrm{г}$).
Правильна відповідь:
90.0
Дві сили, модулі яких дорівнюють відповідно $3 \mathrm{~Н}$ та $4 \mathrm{~Н}$, прикладено до матеріальної точки. Кут між напрямками сил становить $90^{\circ}$. Визначте модуль рівнодійної цих сил.
Відповідь запишіть у ньютонах ($\mathrm{Н}$).
Якщо вантаж $t$ невідомої маси підвісити до короткого плеча важеля, то його можна зрівноважити вантажем масою $400 \mathrm{~г}$. Якщо вантаж $t$ підвісити до довгого плеча важеля, не змінюючи положення точки опори $O$, то його можна зрівноважити вантажем масою $900 \mathrm{~г}$. Масою важеля знехтуйте.
Яка маса $m$ вантажу?
Відповідь запишіть у грамах ($\mathrm{г}$)
Правильна відповідь:
600.0
Спортсмен зробив постріл по мішені. Через $2,25 \mathrm{~c}$ після пострілу він почув звук удару кулі об мішень. Швидкість звуку в повітрі дорівнює $340 \mathrm{~м}/\mathrm{с}$. Рух кулі вважайте рівномірним прямолінійним зі швидкістю $680 \mathrm{~м}/\mathrm{с}$.
Чому дорівнює відношення часу польоту кулі до часу, за який звук удару дійшов від мішені до спортсмена?
По столу тягнуть три зв’язані ниткою бруски, маси яких $m_{1}=2 \mathrm{~кг}$, $m_{2}=3 \mathrm{~кг}$ й $m_{3}=5 \mathrm{~кг}$ (див. рисунок). Кожна з ниток $a, b$ витримує силу натягу до $10 \mathrm{~Н}$ . Визначте максимально можливе значення модуля сили $\vec{F}$. Уважайте, що тертя немає.
Відповідь запишіть у ньютонах ($\mathrm{Н}$).
Правильна відповідь:
20.0
Електровоз рухається рівномірно по горизонтальній прямолінійній ділянці залізниці й тягне вагони загальною масою $2 \cdot 10^{6} \mathrm{~кг}$ із силою $500 \mathrm{~кН}$. З яким прискоренням рухатиметься потяг, якщо сила, з якою електровоз тягне вагони, збільшиться до $600 \mathrm{~кН}$?
Відповідь запишіть у метрах на секунду у квадраті ($\mathrm{м} / \mathrm{с}^{2}$)
Правильна відповідь:
0.05
Усі білі й сірі важки, з яких складено вантажі (див. фото), мають однакову масу. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Тертям у блоці й масою нитки знехтуйте.
Обчисліть модуль прискорення, з яким рухатиметься система, зображена на фотографії, якщо прибрати підставку з-під лівого вантажу.
Відповідь запишіть у метрах за секунду в квадраті ($\mathrm{м} / \mathrm{с}^{2}$).