Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
У коливальному контурі радіоприймача конденсатор електроємністю $C_{1}$ замінили на конденсатор електроємністю $C_{2}$. Як змінився внаслідок цього період вільних електромагнітних коливань у контурі, якщо довжина хвилі, що на неї резонує коливальний контур, змінилася з $6$ на $18 \mathrm{~м}$?
Б
зменшився в $\sqrt{3}$ раз
В
збільшився в 3 рази
Правильна відповідь
В ідеальному коливальному контурі, який складається з конденсатора й котушки індуктивності, максимальний заряд конденсатора збільшили вдвічі. Як зміниться внаслідок цього повна енергія коливального контуру?
Г
збільшиться в 4 рази
Правильна відповідь
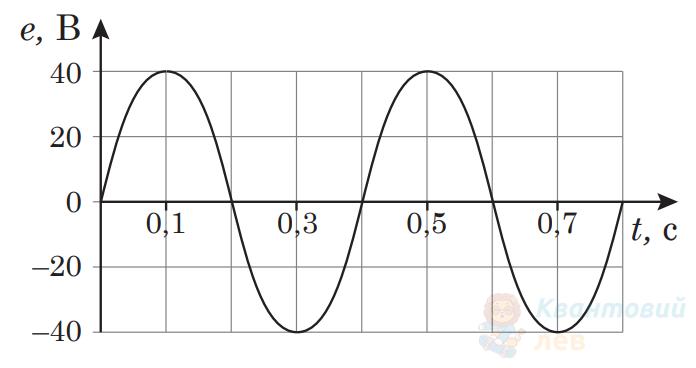
На рисунку наведено графік залежності електрорушійної сили (EPC) $e$ від часу $t$. Якою формулою задано залежність $e$ від $t$, у якій усі значення величин виражено в одиницях SI?
Б
$e=40 \sin 5 \pi t$
Правильна відповідь
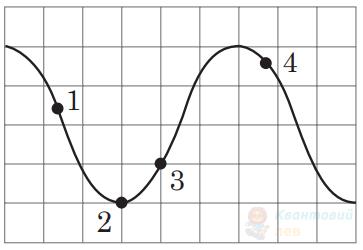
У контурі відбуваються вільні електромагнітні коливання. Коливання напруги на конденсаторі досліджують за допомогою осцилографа, на екрані якого видно зображення залежності напруги від часу. Визначте, яка із зображених точок осцилограми (див. рисунок) відповідає моменту, коли енергія магнітного поля котушки найбільша.
А
точка 1
Правильна відповідь
Заряджений конденсатор приєднали до котушки індуктивності. Чому дорівнює заряд $q$ на пластинах конденсатора ідеального коливального контуру в ту мить, коли від початку коливань пройшло $\frac{3}{4}$ періоду коливань?
А
$q=0$
Правильна відповідь
Б
$q=\frac{1}{4} q_{\max }$
В
$q=\frac{3}{4} q_{\max }$
Індуктивність котушки коливального контуру становить $30 \mathrm{~мкГн}$, а ємність конденсатора – $120 \mathrm{~пФ}$. Визначте (приблизно) довжину електромагнітної хвилі, яка виникає під час роботи цього контуру. Уважайте, що швидкість світла у вакуумі дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}$.
В
$113 \mathrm{~м}$
Правильна відповідь
В ідеальному коливальному контурі відбуваються вільні електромагнітні коливання з періодом $T$. Який із графіків може правильно описувати залежність енергії $W$ електричного поля в конденсаторі від часу $t$ ?
Г
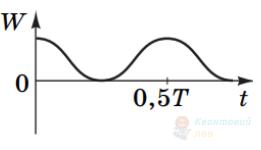Правильна відповідь
В ідеальному коливальному контурі, який складається з конденсатора й котушки індуктивності, максимальну силу струму збільшують удвічі. Як зміниться внаслідок цього період коливань?
Б
не зміниться
Правильна відповідь
В
збільшиться в $\sqrt{2}$ рази
Як зміниться період власних коливань контуру, якщо його індуктивність збільшити у 12 разів, а ємність зменшити в 3 рази?
А
збільшиться у 2 рази
Правильна відповідь
Укажіть, що лежить в основі принципу дії генератора змінного струму.
А
явище електромагнітної індукції
Правильна відповідь
Б
взаємодія постійних магнітів
Частота вільних електромагнітних коливань у контурі дорівнює $1 \mathrm{~кГц}$. Визначте, скільки разів щосекунди сила струму в котушці індуктивності дорівнює нулю.
У коливальному контурі відбуваються вільні електромагнітні коливання. Ємність конденсатора збільшили в 3 рази. Як треба змінити індуктивність котушки контура, щоб період вільних коливань набув попереднього значення?
Б
зменшити в 3 рази
Правильна відповідь
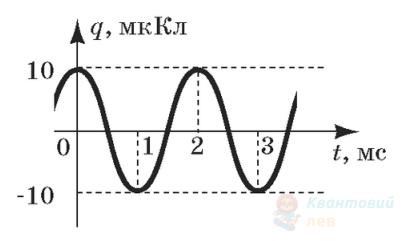
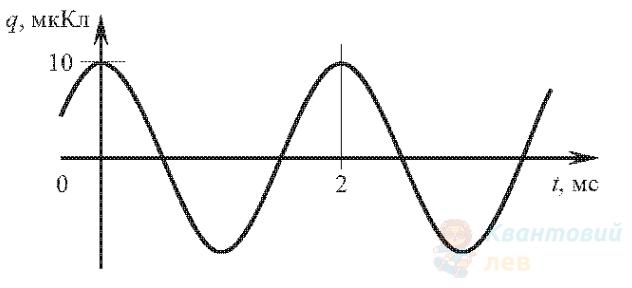
На рисунку зображено графік залежності величини заряду $q$ обкладки конденсатора коливального контуру від часу $t$. Визначте відповідний математичний запис цієї залежності (значення всіх величин наведено в SI).
А
$q=10^{-5} \cdot \sin \left(10^{3} \cdot \pi t\right)$
Б
$q=10^{-5} \cdot \cos \left(10^{-5} \cdot \pi t\right)$
В
$q=10^{-5} \cdot \sin \left(10^{3} \cdot \pi t+\frac{8}{9}\right)$
Правильна відповідь
Г
$q=10^{-5} \cdot \cos \left(10^{3} \cdot \pi t+\frac{8}{9}\right)$
Коливальний контур складається з конденсатора ємністю $0,5 \mathrm{~мкФ}$ і котушки індуктивністю $0,5 \mathrm{~Гн}$. Визначте, яка формула може описувати залежність напруги $u$ на конденсаторі від часу $t$, коли в контурі відбуваються вільні електромагнітні коливання. Усі величини виражено в одиницях SI.
Б
$u=0,5 \cos 2000 t$
Правильна відповідь
Під час незатухаючих електромагнітних коливань при розрядженні конденсатора коливального контуру зменшується
А
модуль магнітної індукції поля котушки.
Б
енергія електричного поля.
Правильна відповідь
Під час вільних незгасаючих електромагнітних коливань у коливальному контурі максимальна сила струму дорівнює $5 \mathrm{~мА}$, а максимальна напруга на конденсаторі – $10 \mathrm{~В}$. Визначте модуль напруги на конденсаторі в момент, коли сила струму в котушці дорівнює $3 \mathrm{~мА}$.
Г
$8 \mathrm{~В}$
Правильна відповідь
Через резистор проходить постійний струм силою $0,1 \mathrm{~А}$, а через лампочку змінний струм частотою $50 \mathrm{~Гц}$, діюче значення якого $0,1 \mathrm{~А}$. Які заряди переносяться через резистор і через лампочку за $2 \mathrm{~хв}$?
А
в обох випадках переноситься заряд $12 \mathrm{~Кл}$
Б
через резистор переноситься заряд $12 \mathrm{~Кл}$, а через лампочку – заряд $50 \mathrm{~Кл}$
В
через резистор переноситься заряд $12 \mathrm{~Кл}$, а через лампочку заряд не переноситься
Правильна відповідь
Г
через резистор переноситься заряд $50 \mathrm{~Кл}$, а через лампочку – заряд $5 \mathrm{~Кл}$
В ідеальному коливальному контурі відбуваються вільні електромагнітні коливання так, що максимальний заряд на обкладках конденсатора дорівнює $q_{m}$, а максимальна сила струму в котушці – $I_{m}$. Який вираз визначає період вільних електромагнітних коливань у контурі?
А
$2 \pi \frac{I_{m}}{q_{m}}$
Б
$2 \pi \frac{q_{m}}{I_{m}}$
Правильна відповідь
В
$2 \pi \sqrt{\frac{q_{m}}{I_{m}}}$
Г
$2 \pi \frac{I_{m}^{2}}{q^{2}}$
Як зміниться період власних коливань контуру, якщо його індуктивність збільшити у 20 разів, а ємність зменшити в 5 разів?
Г
збільшиться у 2 рази
Правильна відповідь
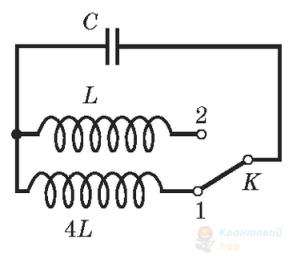
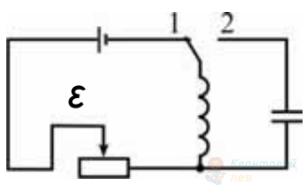
Як зміниться період електромагнітних коливань у контурі, якщо ключ $K$ у колі, схему якого зображено на рисунку, перевести з положення 1 у положення 2?
А
зменшиться у 2 рази
Правильна відповідь
Із наведених формул визначте ту, яка застосовується виключно для описання електромагнітних коливань.
В
$\omega^{2}=1 / L C$
Правильна відповідь
На графіку зображено залежність величини заряду тіла від часу. Визначте відповідний математичний запис цієї залежності.
А
$q=10^{-5} \sin \left(10^{3} \cdot \pi \cdot t\right)$
Б
$q=10^{-5} \cos \left(10^{2} \cdot \pi \cdot t\right)$
Правильна відповідь
В
$q=10^{-5} \sin \left(10^{3} \cdot \pi \cdot t+\pi / 2\right)$
Г
$q=10^{-6} \cos \left(10^{3} \cdot \pi \cdot t\right)$
Частота вільних електромагнітних коливань у контурі дорівнює $20 \mathrm{~кГц}$. Визначте частоту, якщо конденсатор ємністю $0,2 \mathrm{~мкФ}$ замінити конденсатором ємністю $5 \mathrm{~мкФ}$.
Б
$4 \mathrm{~кГц}$
Правильна відповідь
Частота вільних коливань у коливальному контурі з ідеальних конденсатора та котушки дорівнює $2 \mathrm{~кГц}$. Ті самі конденсатор і котушку з'єднали послідовно та підключили до джерела змінного струму. Визначте, як змінюватиметься амплітудне значення сили струму $I_{\text{м}}$ в колі, якщо частоту змінного струму повільно збільшувати від 1 до $3 \mathrm{~кГц}$. Амплітуда напруги є сталою.
А
$I_{\mathrm{м}}$ весь час зростатиме
Б
$I_{\mathrm{м}}$ весь час зменшуватиметься
В
$I_{\mathrm{м}}$ зростатиме, а потім зменшуватиметься
Правильна відповідь
Г
$I_{\mathrm{м}}$ зменшуватиметься, а потім зростатиме
Частота вільних електромагнітних коливань у коливальному контурі дорівнює $1 \mathrm{~кГц}$. Визначте індуктивність котушки контура, якщо ємність конденсатора становить $0,5 \mathrm{~мкФ}$. Уважайте, що $\pi^{2}=10$.
Г
$0,05 \mathrm{~Гн}$
Правильна відповідь
Ідеальний коливальний контур складається з конденсатора ємністю $1 \mathrm{~мкФ}$ та котушки індуктивністю $0,01 \mathrm{~Гн}$. Укажіть, на яку довжину хвилі випромінювання резонує даний контур. Швидкість світла дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}$.
А
$\approx 4 \cdot 10^{6} \mathrm{~м}$
Б
$\approx 1,9 \cdot 10^{6} \mathrm{~м}$
В
$\approx 1,9 \cdot 10^{5} \mathrm{~м}$
Правильна відповідь
Г
$\approx 4 \cdot 10^{5} \mathrm{~м}$
Ідеальний коливальний контур складається з конденсатора ємністю $1 \mathrm{~мкФ}$ та котушки. Визначте індуктивність котушки, якщо даний контур резонує на довжину хвилі випромінювання $1,8 \cdot 10^{5} \mathrm{~м} $. Швидкість світла дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}$.
А
$\approx 0,5 \mathrm{~Гн}$
Б
$\approx 0,1 \mathrm{~Гн}$
В
$\approx 0,05 \mathrm{~Гн}$
Г
$\approx 0,01 \mathrm{~Гн}$
Правильна відповідь
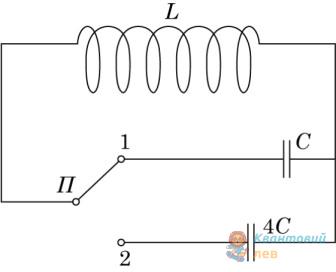
Ідеальний коливальний контур містить котушку індуктивності $L$ і два конденсатори, електроємність яких $C$ й $4C$. За допомогою перемикача $П$ можна приєднати до котушки кожен конденсатор окремо (див. рисунок).
Як зміниться частота власних коливань у контурі, якщо перевести перемикач з положення 1 у положення 2?
Б
зменшиться вдвічі
Правильна відповідь
Конденсатору електроємністю $0,01 \mathrm{~мкФ}$, який є складником коливального контуру, надали заряд $4 \cdot 10^{-4} \mathrm{~Кл}$. У цьому контурі відбуваються електромагнітні коливання, що згасають. Яка кількість теплоти виділиться в контурі до моменту часу, коли коливання повністю згаснуть? Уважайте, що контур не випромінює електромагнітні хвилі. Відповідь запишіть у джоулях ($\mathrm{Дж}$).
За рівномірної зміни сили струму на $1,2 \mathrm{~А}$ в котушці індуктивності за $0,6$ секунди виникає електрорушійна сила (ЕРС) самоіндукції, що дорівнює $0,2 \mathrm{~мВ}$. Визначте довжину радіохвилі, випромінюваної антеною генератора, коливальний контур якого складається із цієї котушки та конденсатора ємністю $10 \mathrm{~пФ}$. Уважайте, що швидкість світла в повітрі дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}$, $\pi^{2}=10$.
Відповідь запишіть у метрах ($\mathrm{м}$).
Правильна відповідь:
60.0
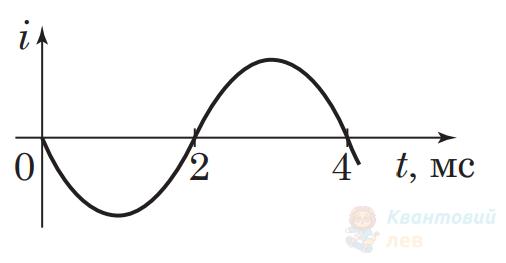
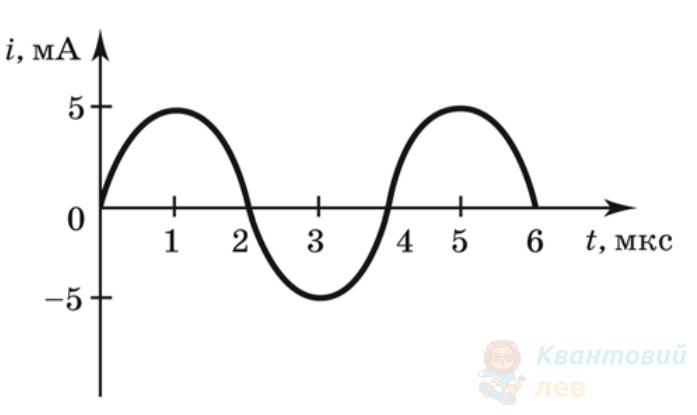
У коливальному контурі відбуваються вільні електромагнітні коливання. На рисунку зображено графік залежності сили струму $i$ від часу $t$. Індуктивність котушки контуру дорівнює $50 \mathrm{~мГн}$.
Визначте період коливань сили струму в контурі.
Відповідь запишіть у мілісекундах ($\mathrm{мс}$).
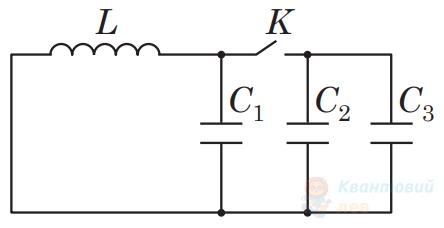
На рисунку зображено схему електричного кола, яке складається з котушки індуктивності $L$, батареї конденсаторів та ключа $K$. Уважайте, що електроємності конденсаторів становлять $C_{1}=0,5 \mathrm{~мкФ}$, $C_{2}=1,5 \mathrm{~мкФ}$, $C_{3}=2,5 \mathrm{~мкФ}$.
У скільки разів збільшиться період вільних електромагнітних коливань у контурі, якщо ключ $K$ в колі, схему якого зображено на рисунку, замкнути.
Індуктивність котушки коливального контуру $25 \mathrm{~мкГн}$, а ємність конденсатора $3600 \mathrm{~пФ}$. Визначте довжину електромагнітної хвилі, яка виникає під час роботи цього контуру. Уважайте, що швидкість світла у вакуумі становить $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}, \pi=3,1$.
Відповідь запишіть у метрах ($\mathrm{м}$).
Правильна відповідь:
558.0
Параметри першого коливального контуру такі: електроємність конденсатора $C_{1}=36 \mathrm{~нФ}$, індуктивність котушки $L_{1}=16 \mathrm{~мГн}$. Якою має бути індуктивність $L_{2}$ котушки другого контуру, щоб він був настроєний на ту саму частоту, що й перший? Електроємність конденсатора другого контуру $C_{2}=24 \mathrm{~нФ}$.
Відповідь запишіть у мілігенрі ($\mathrm{мГн}$).
Правильна відповідь:
24.0
Коливальний контур радіоприймача складається з котушки індуктивністю $0,27 \mathrm{~мГн}$ та конденсатора змінної ємності. Контур може налаштовуватися на хвилі довжиною від $188 \mathrm{~м}$ до $540 \mathrm{~м}$. Визначте максимальну ємність конденсатора. Уважайте, що $\pi^{2}=10$, швидкість поширення електромагнітної хвилі у вакуумі дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}$.
Відповідь запишіть у пікофарадах ($\mathrm{пФ}$)
Правильна відповідь:
300.0
Частота вільних електромагнітних коливань у контурі дорівнює $1 \mathrm{~кГц}$.
Визначте період електромагнітних коливань у контурі.
Відповідь запишіть у секундах ($\mathrm{с}$)
Правильна відповідь:
0.001
До котушки індуктивності під’єднали заряджений конденсатор. У колі виникли електромагнітні коливання. Індуктивність котушки $10 \mathrm{~мГн}$, ємність конденсатора $40 \mathrm{~мФ}$. Активним опором кола знехтуйте.
Визначте циклічну частоту електромагнітних коливань.
Відповідь запишіть у радіанах за секунду ($\mathrm{рад}/\mathrm{с}$)
Правильна відповідь:
50.0
Ідеальний коливальний контур складається з конденсатора ємністю $1 \mathrm{~нФ}$ та котушки. Визначте індуктивність котушки, якщо цей контур резонує на довжину хвилі випромінювання $180 \mathrm{~м}$. Уважайте, що швидкість світла дорівнює $3 \cdot 10^{8} \mathrm{~м} / \mathrm{с}, \pi^{2}=10$.
Відповідь запишіть у мікрогенрі ($\mathrm{мкГн}$).
У контурі, що складається з конденсатора й котушки індуктивності, відбуваються коливання. Обчисліть, яку частку (%) від максимального значення становить заряд на конденсаторі в той момент часу, коли значення струму, що проходить крізь котушку, становить $80 \%$ від максимально можливого.
Правильна відповідь:
60.0
В ідеальному коливальному контурі амплітуда коливань сили струму в котушці індуктивності дорівнює $5 \mathrm{~мА}$ , амплітуда коливань заряду конденсатора становить $5 \mathrm{~нКл}$. У момент часу $t$ заряд конденсатора дорівнює $3 \mathrm{~нКл}$. Визначте силу струму в котушці в цей момент. Відповідь запишіть у міліамперах.
На рисунку зображено графік залежності сили струму від часу в коливальному контурі під час вільних коливань. Визначте, яким стане період коливань у контурі, якщо ємність конденсатора збільшити в 4 рази.
Відповідь запишіть у мікросекундах.
У електричному колі, зображеному на рисунку, внутрішній опір джерела струму дорівнює $1 \mathrm{~Ом}$, повний опір реостата дорівнює $6 \mathrm{~Ом}$, активний опір котушки дорівнює $2 \mathrm{~Ом}$. Спочатку ковзний контакт реостата знаходився в крайньому лівому положенні, а ключ – у положенні 1. Коли ключ перевели в положення 2, у конденсаторі та котушці виникли вільні електромагнітні коливання. Визначте, у скільки разів збільшиться початкова амплітуда коливань, якщо встановити опір реостата рівним $3 \mathrm{~Ом}$ та повторити дослід.
За час, протягом якого амплітуда вільних електромагнітних коливань у коливальному контурі зменшилася втричі, у контурі виділилася кількість теплоти, що дорівнює $64 \mathrm{мДж}$. Визначте кількість теплоти, яка виділиться під час зменшення амплітуди коливань ще удвічі. Відповідь запишіть у міліджоулях.
