Подібні питання (17)
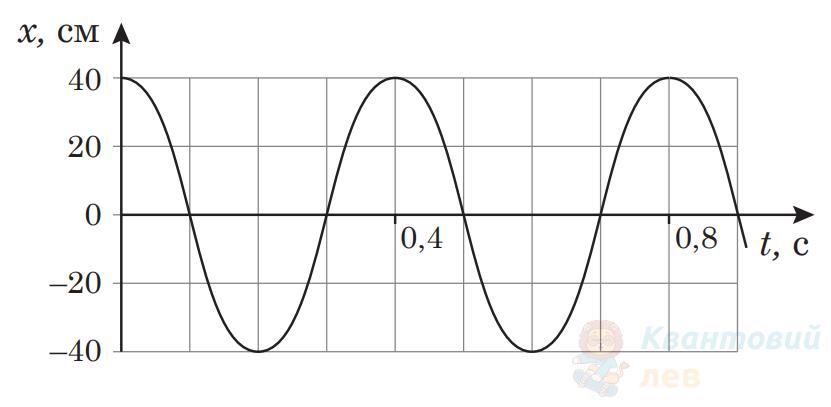
На рисунку зображено графік залежності координати $x$ тіла, що здійснює гармонічні коливання вздовж осі $O x$, від часу $t$. Якою формулою задано залежність $x$ від $t$, якщо значення всіх величин виражено в одиницях SI?
Г
$x=0,4 \cos 5 \pi t$
Правильна відповідь
Координата точки, що здійснює гармонічні коливання, змінюється залежно від часу за законом $x=0,05 \sin (20 \pi t+0,8)$, де всі величини виражено в одиницях SI. Визначте частоту коливань.
В
$10 \mathrm{~Гц}$
Правильна відповідь
Точка здійснює гармонічні коливання за законом $x=A \cos (\omega t+\varphi)$. У певний момент часу зміщення точки – $x_{1}=5 \mathrm{~см}$, її швидкість – $v_{1}=20 \mathrm{~см} / \mathrm{с}$, а прискорення – $a_{1}=-80 \mathrm{~см} / \mathrm{с}^{2}$. Визначте циклічну частоту коливань.
А
$2 \mathrm{~рад}/\mathrm{с}$
Б
$4 \mathrm{~рад}/\mathrm{с}$
Правильна відповідь
В
$8 \mathrm{~рад}/\mathrm{с}$
Г
$10 \mathrm{~рад}/\mathrm{с}$
Тіло здійснює гармонічні коливання з частотою $100 \mathrm{~Гц}$. Амплітуда коливань дорівнює $5 \cdot 10^{-3} \mathrm{~м}$. Визначте максимальне значення прискорення тіла. Вважайте, що $\pi^{2}=10$.
А
$500 \mathrm{~м} / \mathrm{с}^{2}$
Б
$2000 \mathrm{~м} / \mathrm{с}^{2}$
Правильна відповідь
В
$1800 \mathrm{~м} / \mathrm{с}^{2}$
Г
$100 \mathrm{~м} / \mathrm{с}^{2}$
Тягарець масою $50 \mathrm{~г}$ здійснює вільні коливання на пружині жорсткістю $20 \mathrm{~H} / \mathrm{м}$. У початковий момент часу відхилення від положення рівноваги є максимальним і дорівнює $3 \mathrm{~см}$. Укажіть рівняння, яким описано рух маятника. Усі значення величин у рівняннях виражено в одиницях SI.
В
$x=0,03 \cos 20 t$
Правильна відповідь
Координата тіла, що здійснює гармонічні коливання вздовж осі $O X$, змінюється за законом $x=0,9 \sin (3 t)$, де всі величини виражено в одиницях SI. Визначте частоту коливань прискорення тіла.
А
$\frac{3 t}{2 \pi} \mathrm{~Гц}$
Б
$\frac{2 \pi}{3} \mathrm{~Гц}$
Г
$\frac{3}{2 \pi} \mathrm{~Гц}$
Правильна відповідь
Амплітуда коливань тіла на пружині дорівнює $0,5 \mathrm{~м}$. Визначте шлях, який пройшло це тіло за п’ять періодів коливань.
А
$10 \mathrm{~м}$
Правильна відповідь
Тіло здійснює гармонічні коливання з періодом $T=2$ с. Протягом половини періоду коливань через рівні проміжки часу виміряли (у см) зміщення $x$ тіла й одержали такі значення: $1 ; 0,7 ; 0 ;-0,7 ;-1$. У якому рядку записано послідовність моментів часу (у секундах), що відповідає вказаній послідовності значень зміщення тіла? Уважайте, що $\sqrt{2}=1,4$.
А
$0 ;\ 0,5 ;\ 1 ;\ 1,5 ;\ 2$
Б
$0 ;\ 0,25 ;\ 0,5 ;\ 0,75 ;\ 1$
Правильна відповідь
В
$90 ;\ 135 ;\ 180 ;\ 225 ;\ 270$
Г
$0 ;\ 45 ;\ 90 ;\ 135 ;\ 180$
Тіло масою $0,5 \mathrm{~кг}$ коливається так, що проєкція прискорення $a_{x}$ його руху змінюється з часом відповідно до рівняння $a_{x}=6 \sin \frac{2 \pi}{10} t$. Визначте проєкцію на вісь $O x$ сили, що діє на тіло, у момент часу $\frac{5}{6} \mathrm{с}$.
Б
$1,5 \mathrm{~Н}$
Правильна відповідь
Залежності деяких величин від часу $t$ мають вигляд
$x_{1}=0,01 \sin \left(2 t+\frac{5}{3}\right)$;
$x_{2}=0,1 \sin \left(2 t^{2}\right)$;
$x_{3}=0,01 \sin \left(3 \sqrt{t}\right)$;
$x_{4}=0,05 t \cdot \sin \left(3 t+\frac{5}{4}\right)$.
Яка з цих величин змінюється за законом гармонічних коливань?
А
$x_{1}$
Правильна відповідь
Визначте, яка залежність координати тіла $x$ від часу $t$ описує прямолінійний рівноприскорений рух уздовж осі $O x$ з початковою швидкістю $6 \mathrm{~м}/\mathrm{с}$ та прискоренням $1 \mathrm{~м}/ \mathrm{с}^{2}$. Усі величини у формулах виражено в одиницях SI.
В
$x=1+6 t+0,5 t^{2}$
Правильна відповідь
Початкова координата тіла, що рухається вздовж осі $Ox$, дорівнює $10 \mathrm{~м}$, прискорення, з яким рухається тіло, становить $5 \mathrm{~м} / \mathrm{с}^{2}$, а початкова швидкість руху дорівнює $2,5 \mathrm{~м} / \mathrm{с}$. Яке рівняння, що описує рух тіла, може відповідати цим умовам?
Усі значення величин у рівняннях наведено в одиницях SI.
А
$x=10+2,5 t+2,5 t^{2}$
Правильна відповідь
Коливальний контур складається з конденсатора ємністю $0,5 \mathrm{~мкФ}$ і котушки індуктивністю $0,5 \mathrm{~Гн}$. Визначте, яка формула може описувати залежність напруги $u$ на конденсаторі від часу $t$, коли в контурі відбуваються вільні електромагнітні коливання. Усі величини виражено в одиницях SI.
Б
$u=0,5 \cos 2000 t$
Правильна відповідь
Швидкість тіла масою $0,8 \mathrm{~кг}$, що рухається вздовж осі $O X$, змінюється відповідно до рівняння $v_{x}=0,05 \sin (10 \pi t)$, де всі величини виражено в одиницях SI. Визначте імпульс тіла через $0,2 \mathrm{~c}$ після початку відліку часу.
А
$0 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
Правильна відповідь
Б
$0,001 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
В
$0,002 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
Г
$0,04 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$
Тіло рухається прямолінійно так, що модуль швидкості його руху протягом усього часу збільшується. Яким із-поміж наведених рівнянь залежності координати $x$ тіла від часу $t$ можна описати цей рух? Усі значення величин у рівняннях виражено в одиницях SI. Уважайте, що вісь координат $O x$ паралельна траєкторії руху тіла.
А
$x=5-2 t^{2}$
Правильна відповідь
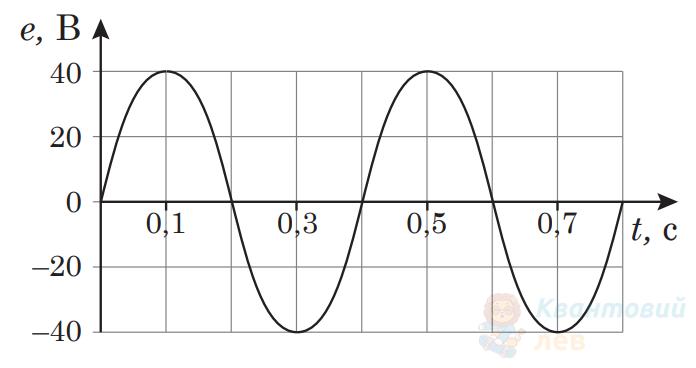
На рисунку наведено графік залежності електрорушійної сили (EPC) $e$ від часу $t$. Якою формулою задано залежність $e$ від $t$, у якій усі значення величин виражено в одиницях SI?
Б
$e=40 \sin 5 \pi t$
Правильна відповідь
Яке з наведених рівнянь рухів уздовж осі $O x$ тіл з однаковими масами відповідає руху тіла з найбільшою кінетичною енергією? Усі значення величин у рівняннях виражено в одиницях SI ($x$ – координата тіла, $t$ – час).
Б
$x=5-10 t$
Правильна відповідь