Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
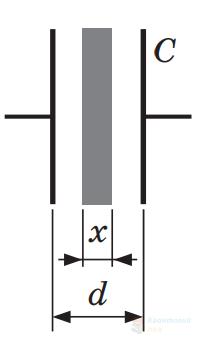
На рисунку схематично зображено конденсатор. Відстань між його пластинами – $d$, площа кожної пластини конденсатора – $S$. Який із наведених графіків може відображати залежність електроємності $C$ конденсатора від товщини $x$ діелектрика, установленого між пластинами?
А
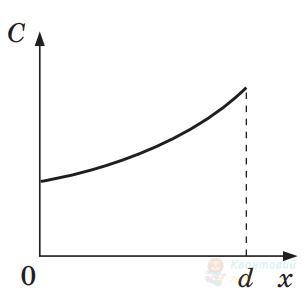 Правильна відповідь
Правильна відповідь
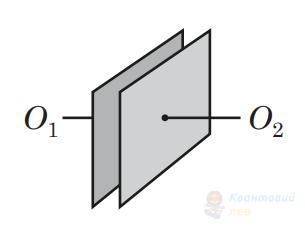
Обкладками плоского повітряного конденсатора, зображеного на рисунку, є дві квадратні металеві пластини. У який спосіб можна збільшити електричну ємність цього конденсатора?
А
Змістити одну з пластин трохи вгору
Б
Зменшити відстань між пластинами
Правильна відповідь
В
Повернути одну з пластин на $45^{\circ}$ навколо осі $O_{1} O_{2}$
Г
Збільшити відстань між пластинами
Проводячи дослідження, у першому випадку в заряджений і відключений від батарейки плоский повітряний конденсатор поміщають слюдяну пластинку так, що вона займає весь простір між пластинами конденсатора. У другому випадку розсовують пластини конденсатора, при цьому простір між ними залишається заповненим повітрям. Діелектрична проникність слюди вшестеро більша, ніж діелектрична проникність повітря. Напруженість поля в просторі між пластинами
А
в обох випадках не змінюється.
Б
в обох випадках збільшується.
В
у першому випадку зменшується, у другому – збільшується.
Г
у першому випадку зменшується, у другому – не змінюється.
Правильна відповідь
Як зміниться ємність плоского повітряного конденсатора, якщо його опустити в гліцерин, діелектрична проникність якого становить 7? Діелектрична проникність повітря дорівнює 1 .
А
збільшиться в 7 разів
Правильна відповідь
Плоский повітряний конденсатор зарядили та від'єднали від джерела струму. У конденсаторі установилася напруженість $E_{0}$. Яка буде напруженість електричного поля всередині конденсатора, якщо відстань між пластинами збільшити вдвічі?
А
$E_{0}$
Правильна відповідь
Б
$\frac{\sqrt{2}}{2} E_{0}$
Заряджений плоский конденсатор від'єднали від джерела струму та зменшили відстань між його пластинами. Які величини зазнали змін?
А
заряд конденсатора і його електроємність
Б
заряд конденсатора і напруженість електричного поля
В
напруженість електричного поля і напруга між пластинами
Г
електроємність і напруга між пластинами
Правильна відповідь
Два плоскі повітряні конденсатори однакової електричної ємності з'єднані послідовно, як зображено на рисунку. Як зміниться ємність системи конденсаторів, якщо їх занурити в гліцерин? Уважайте, що діелектрична проникність гліцерину дорівнює 42.
А
збільшиться в 42 рази
Правильна відповідь
Конденсатор складається з двох круглих металевих пластин радіусом $10 \mathrm{~см}$, між якими розташовано пластину текстоліту товщиною $6,28 \mathrm{~мм}$ такого самого радіуса. Під час вимірювання електроємності фарадометр показав значення $C=308 \mathrm{~пФ}$ (див. рисунок). Визначте діелектричну проникність текстоліту. Уважайте, що електрична стала $\varepsilon_{0}$ дорівнює $8,8 \cdot 10^{-12} \mathrm{~Ф} / \mathrm{м}$.
Пластини плоского конденсатора, кожна з яких має площу $100 \mathrm{~см}^{2}$, розташовані на відстані $2 \mathrm{~мм}$ одна від одної. Напруга на конденсаторі становить $40 \mathrm{~В}$. Уважайте, що електрична стала дорівнює $9 \cdot 10^{-12} \mathrm{~Ф} / \mathrm{м}$, а діелектрична проникність повітря становить 1.
Визначте електроємність конденсатора.
Відповідь запишіть у пікофарадах ($\mathrm{пФ}$)
Правильна відповідь:
45.0
Пластини плоского конденсатора, кожна з яких має площу $100 \mathrm{~см}^{2}$, розташовані на відстані $2 \mathrm{~мм}$ одна від одної. Напруга на конденсаторі становить $40 \mathrm{~В}$. Уважайте, що електрична стала дорівнює $9 \cdot 10^{-12} \mathrm{~Ф} / \mathrm{м}$, а діелектрична проникність повітря становить 1.
Визначте енергію, що виділиться під час розряджання цього конденсатора.
Відповідь запишіть у наноджоулях ($\mathrm{нДж}$)
Правильна відповідь:
36.0
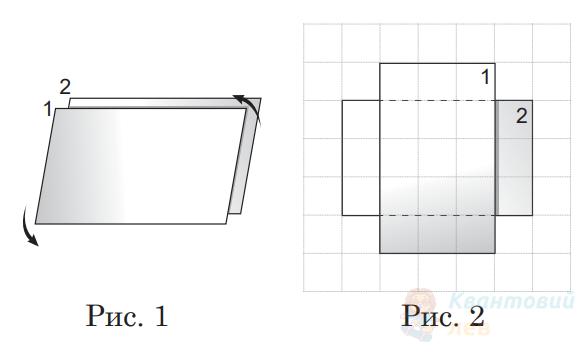
Обкладками плоского повітряного конденсатора є дві паралельні прямокутні металеві пластини 1 та 2, які спочатку розміщені одна напроти одної (див. рисунок 1). Пластину 1 повернули на $90^{\circ}$, як показано на рисунку 2.
Визначте відношення кінцевої електроємності конденсатора до початкової.