Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
Укажіть ситуацію, у якій вага тіла більша за силу тяжіння, що діє на тіло.
А
автомобіль, рухаючись рівномірно, перебуває у верхній точці опуклого мосту
Б
космонавт перебуває в ракеті під час її старту з поверхні Землі
Правильна відповідь
В
камінь падає з деякої висоти
Г
людина починає опускатися разом із кабіною ліфта
Однорідне тіло плаває в товщі рідини. Укажіть співвідношення між модулями сили Архімеда $F_{\mathrm{A}}$ й сили тяжіння $m g$, що діють на тіло, і співвідношення між густиною тіла $\rho_{\mathrm{т}}$ й густиною рідини $\rho_{\mathrm{p}}$, які правильно описують «поведінку» цього тіла.
А
$F_{\mathrm{A}} < m g, \rho_{\mathrm{т}} > \rho_{\mathrm{p}}$
Б
$F_{\mathrm{A}} = m g, \rho_{\mathrm{т}} = \rho_{\mathrm{p}}$
Правильна відповідь
В
$F_{\mathrm{A}} > m g, \rho_{\mathrm{т}} < \rho_{\mathrm{p}}$
Г
$F_{\mathrm{A}} = m g, \rho_{\mathrm{т}} < \rho_{\mathrm{p}}$
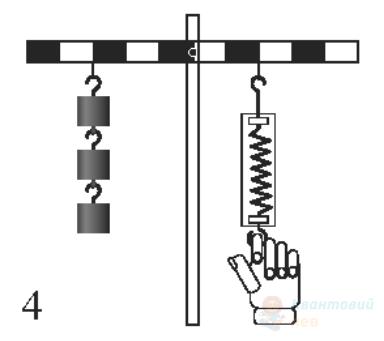
Важіль, зображений на рисунку, перебуває в рівновазі. Маса кожного тягарця становить $100 \mathrm{~г}$. Визначте показ динамометра. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$4,5 \mathrm{~H}$
Правильна відповідь
Тіло рівномірно зісковзує з похилої площини. Визначте, які співвідношення правильні для роботи сили тяжіння $A_{\text{тяж}}$ і роботи сили тертя $A_{\text{тер}}$ (силу опору повітря не враховуйте).
А
$A_{\text{тяж}}=A_{\text{тер}}=0$
Б
$A_{\text{тяж}}=A_{\text{тер}}>0$
В
$A_{\text{тяж}}=-A_{\text{тер}}>0$
Правильна відповідь
Г
$A_{\text{тяж}}=-A_{\text{тер}}<0$
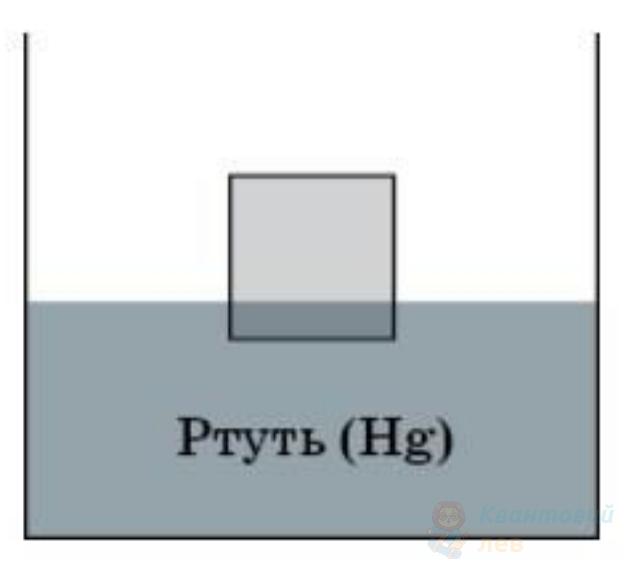
У посудині зі ртуттю плаває суцільний металевий кубик. Він на $1 / 5$ частину свого об’єму занурений у ртуть (див. рисунок). Використавши наведені в таблиці округлені дані щодо густини металів, укажіть метал, з якого виготовлено кубик.
Б
$\mathrm{Al}$
Правильна відповідь
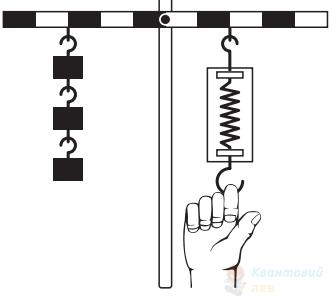
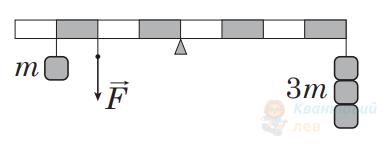
На рисунку зображено важіль, до якого підвішено тягарці масою ( $m$ ) $100 \mathrm{~г}$ кожний. Якою є сила натягу нитки $\vec{F}$, якщо важіль перебуває в рівновазі? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
В
$4,5\mathrm{~Н}$
Правильна відповідь
Система складається з нерухомого блока, через який перекинуто нитку, до кінців якої прив'язано квадратні шматки жерсті. Шматки виготовлені з однакового матеріалу та мають однакову товщину. Сторона одного шматка у два рази більша, ніж сторона другого. З яким прискоренням рухатиметься система? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Tepтям знехтуйте.
А
$2 \mathrm{~м} / \mathrm{с}^{2}$
Б
$4 \mathrm{~м} / \mathrm{с}^{2}$
В
$6 \mathrm{~м} / \mathrm{с}^{2}$
Правильна відповідь
Г
$8 \mathrm{~м} / \mathrm{с}^{2}$
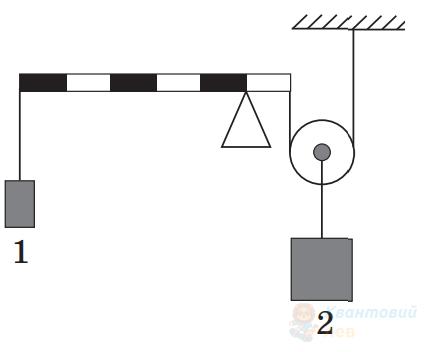
Точка опори ділить важіль у співвідношенні $1:5$. Якою є маса вантажу 2, якщо важіль перебуває в рівновазі? Маса вантажу 1 становить $30 \mathrm{~кг}$. Масами блока та важеля, а також тертям у блоці знехтуйте.
Г
$300 \mathrm{~кг}$
Правильна відповідь
Коли брусок плаває в гасі, його нижня грань знаходиться нижче рівня рідини на $60 \mathrm{~мм}$. Визначте, на якій глибині знаходиться нижня грань того самого бруска, коли він плаває у воді. Уважайте, що густина гасу дорівнює $800 \mathrm{~кг} / \mathrm{м}^{3}$, густина води – $1000 \mathrm{~кг} / \mathrm{м}^{3}$.
Б
$48 \mathrm{~мм}$
Правильна відповідь
Вертикальна циліндрична посудина з гелієм (молярна маса гелію дорівнює $4 \mathrm{~г}/\mathrm{моль}$), що зверху закрита легкорухомим поршнем масою $4 \mathrm{~кг}$, знаходиться в повітрі, тиск якого становить $100 \mathrm{~кПа}$. Маса гелію дорівнює $16 \mathrm{~г}$, площа поперечного перерізу поршня становить $20 \mathrm{~см}^{2}$. Визначте, на скільки збільшиться об'єм, який займе газ, якщо його нагріти на $6 \mathrm{~К}$. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$; універсальна газова стала дорівнює $8,3 \mathrm{~Дж} / ( \mathrm{моль} \cdot \mathrm{К} )$.
Г
$1660 \mathrm{~см}^{3}$
Правильна відповідь
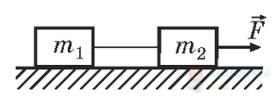
На столі знаходяться два бруски масами $m_{1} = 1 \mathrm{~кг}$ і $m_{2} = 2 \mathrm{~кг}$, зв'язані невагомою нерозтяжною ниткою (див. рисунок). Коефіцієнти тертя між брусками та столом відповідно дорівнюють $\mu_{1}=0,5$ і $\mu_{2}=0,3$. До другого бруска прикладають горизонтальну силу $\vec{F}$, модуль якої дорівнює $8 \mathrm{~Н}$ . Визначте силу натягу нитки. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
А
$2 \mathrm{~Н}$
Правильна відповідь
Важок, який висить нерухомо на пружині, розтягує її на $\Delta x = 9 \mathrm{~см}$. Чому дорівнюватиме період вертикальних коливань важка на пружині? Уважайте, що $\sqrt{10} = \pi$.
А
$0,6 \mathrm{~с}$
Правильна відповідь
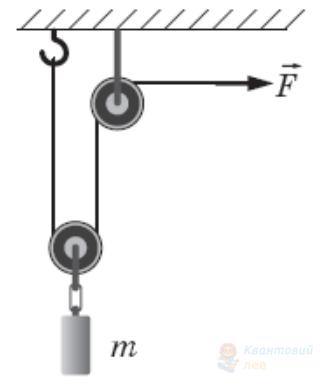
За допомогою системи блоків рівномірно піднімають вантаж масою $m=4 \mathrm{~кг}$, прикладаючи силу $F=25 \mathrm{H}$ (див. рисунок). Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$. Коефіцієнт корисної дії такого механізму дорівнює
Г
$80\ \%$
Правильна відповідь
Для визначення поверхневого натягу рідини використали вертикально розміщену піпетку, радіус отвору якої становить $1 \mathrm{~мм}$. Загальна маса 100 крапель, що витекли з піпетки, дорівнює $12,56 \mathrm{~г}$. Визначте поверхневий натяг рідини. Вважайте, що в момент відриву від піпетки діаметр шийки краплі дорівнює діаметру отвору. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2} ; \pi=3,14$.
А
$100 \mathrm{~мH} / \mathrm{м}$
Б
$200 \mathrm{~мH} / \mathrm{м}$
Правильна відповідь
В
$314 \mathrm{~мH} / \mathrm{м}$
Г
$628 \mathrm{~мH} / \mathrm{м}$
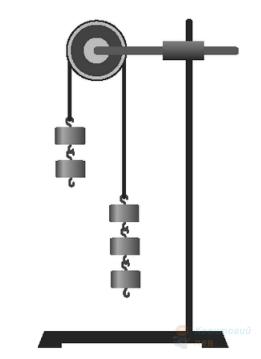
На рисунку зображено однакові тягарці, прив'язані до кінців легкої нерозтяжної нитки, яку перекинуто через нерухомий блок. Визначте модуль прискорення руху тягарців. Тертям і масою блоку знехтуйте. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
А
$2 \mathrm{~м} / \mathrm{с}^{2}$
Правильна відповідь
Б
$3,3 \mathrm{~м} / \mathrm{с}^{2}$
В
$5 \mathrm{~м} / \mathrm{с}^{2}$
Г
$6,6 \mathrm{~м} / \mathrm{с}^{2}$
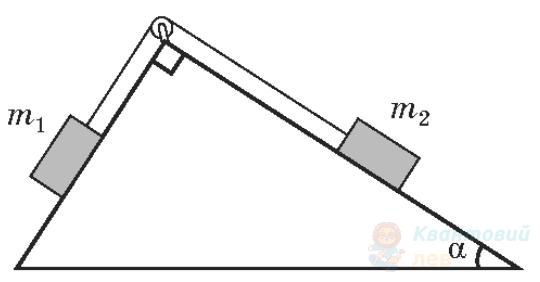
Зображена на рисунку система перебуває в рівновазі. Тертя немає. Визначте співвідношення мас брусків. Нитку вважайте невагомою і нерозтяжною.
А
$\frac{m_{1}}{m_{2}}=\sin \alpha$
Б
$\frac{m_{1}}{m_{2}}=\cos \alpha$
В
$\frac{m_{1}}{m_{2}}=\operatorname{tg} \alpha$
Правильна відповідь
Г
$\frac{m_{1}}{m_{2}}=\operatorname{ctg} \alpha$
Визначте масу вантажу, підвішеного до блока. Масою блока знехтуйте. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$10 \mathrm{~кг}$
Правильна відповідь
Бетонну плиту масою $200 \mathrm{~кг}$ піднімають підйомним краном рівномірно зі швидкістю $0,5 \mathrm{~м}/\mathrm{с}$. Чому дорівнює в цей час вага плити? Прискорення вільного падіння вважайте рівним $10 \mathrm{~м}/\mathrm{с}^2$.
Б
$2000 \mathrm{~Н}$
Правильна відповідь
Деталь має форму двох з'єднаних разом циліндрів із різними діаметрами. Її підвішують на нитці над посудиною, у яку починають повільно наливати воду. На якому з графіків правильно відображено залежність сили натягу нитки від висоти рівня рідини?
А
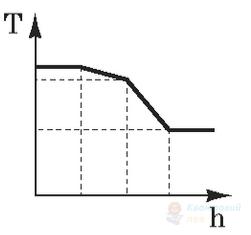Правильна відповідь
Кулька, підвішена на пружині, здійснює вертикальні коливання. Розглянемо три точки траєкторії руху: верхню точку, середню та нижню. У якій із цих точок сили, що діють на кульку, урівноважують одна одну?
Б
у середній
Правильна відповідь
Г
у жодній із зазначених точок
Однорідну кулю підвісили на пружині. Після занурення системи в масло (густина масла дорівнює $900 \mathrm{~кг} / \mathrm{м}^{3}$) видовження пружини зменшилося в 3 рази. Визначте густину матеріалу кулі.
А
$600 \mathrm{~кг} / \mathrm{м}^{3}$
Б
$1350 \mathrm{~кг} / \mathrm{м}^{3}$
Правильна відповідь
В
$1750 \mathrm{~кг} / \mathrm{м}^{3}$
Г
$2700 \mathrm{~кг} / \mathrm{м}^{3}$
Важіль (1) без тертя може вільно обертатися навколо осі (2). Спочатку за відсутності важків та вантажу (3) важіль було зрівноважено. Визначте масу вантажу (3).
Б
$0,5 \mathrm{~кг}$
Правильна відповідь
Визначте масу бруска, що висить на нитці. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
В
$90 \mathrm{~г}$
Правильна відповідь
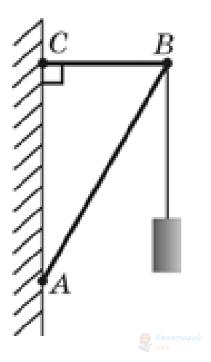
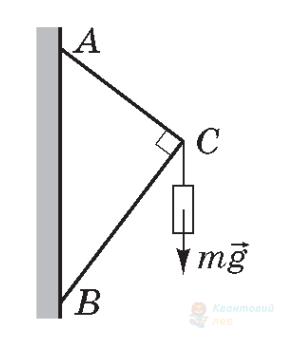
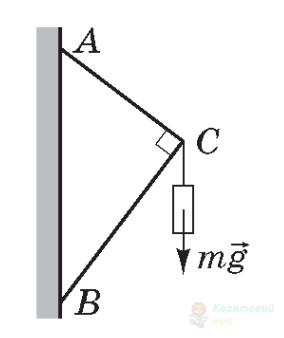
Вантаж масою $5,19 \mathrm{~кг}$ підвішено до невагомих стержнів (див. рисунок). 3'єднання в точках $A, B, C$ є шарнірними. Довжина стержня $A B$ становить $70 \mathrm{~см}$, довжина стержня $B C-35 \mathrm{~см}$. Визначте силу, що стискає стержень $A B$. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}, \sqrt{3}=1,73$.
Г
$60 \mathrm{~Н}$
Правильна відповідь
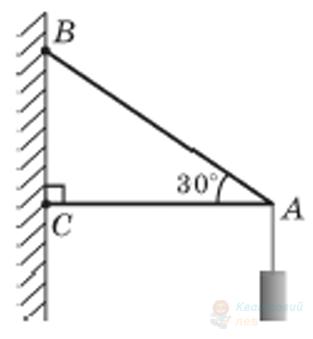
Вантаж масою $2,25 \mathrm{~кг}$ підвішено до невагомих стержнів (див. рисунок). З'єднання у точках $A, B, C$ є шарнірними. Кут $B A C$ дорівнює $30^{\circ}$. Визначте силу, що розтягує стержень $A B$. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$45 \mathrm{~Н}$
Правильна відповідь
Мідний провідник, маса якого дорівнює $2 \mathrm{~г}$, довжина – $10 \mathrm{~см}$, уміщений горизонтально в однорідне магнітне поле з індукцією $20 \mathrm{~мТл}$. Вектор магнітної індукції горизонтальний і перпендикулярний до провідника. Визначте силу струму, яка повинна бути у провіднику, щоб він «завис» у магнітному полі. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Б
$10 \mathrm{~А}$
Правильна відповідь
Визначте, яку загальну масу має смугастий циліндричний вантаж. Призматичні вантажі на фото мають масу по $100 \mathrm{~г}$ кожен.
Д
$500 \mathrm{~г}$
Правильна відповідь
Провідник, кожен метр якого має масу $10 \mathrm{~г}$, завис в однорідному магнітному полі перпендикулярно до його силових ліній. Визначте індукцію магнітного поля, коли сила струму в провіднику дорівнює $10 \mathrm{~А}$. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$0,01 \mathrm{~Тл}$
Правильна відповідь
Повітряну кулю об'ємом $200 \mathrm{~м}^{3}$ наповнено теплим повітрям. Куля з підвішеним до неї вантажем плаває на невеликій висоті над землею, де густина зовнішнього повітря дорівнює $1,3 \mathrm{~кг}/\mathrm{м}^{3}$. Загальна маса оболонки кулі та вантажу, що підвішений до кулі, становить $100 \mathrm{~кг}$. Визначте густину повітря всередині кулі.
А
$1,25 \mathrm{~кг} / \mathrm{м}^{3}$
Б
$0,8 \mathrm{~кг} / \mathrm{м}^{3}$
Правильна відповідь
В
$0,5 \mathrm{~кг} / \mathrm{м}^{3}$
Г
$0,05 \mathrm{~кг} / \mathrm{м}^{3}$
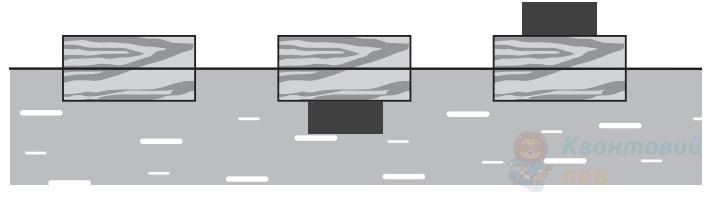
Спочатку брусок, навантажений тягарцями, рівномірно тягли по горизонтальній рейці (див. фото 1). Потім цей брусок разом з тягарцями зважили (див. фото 2). Визначте за результатами вимірювань коефіцієнт тертя між бруском і рейкою.
Товщина крижини дорівнює $40 \mathrm{~см}$, а її площа – $8 \mathrm{~м}^{2}$. Визначте максимальну масу вантажу, з яким крижина може плавати в озері так, щоб вантаж залишався над поверхнею води. Густина льоду становить $900 \mathrm{~кг} / \mathrm{м}^3$, а густина води дорівнює $1000 \mathrm{~кг} / \mathrm{м}^3$.
Г
$320 \mathrm{~кг}$
Правильна відповідь
У рідину занурили одним кінцем відкриту вертикальну трубку радіусом $0,32 \mathrm{~мм}$. Визначте вагу рідини, яка підніметься у трубці за умови повного змочування. Поверхневий натяг рідини дорівнює $0,05 \mathrm{~H} / \mathrm{м}$. Уважайте, що $\pi=25 / 8$.
Б
$0,1 \mathrm{~мH}$
Правильна відповідь
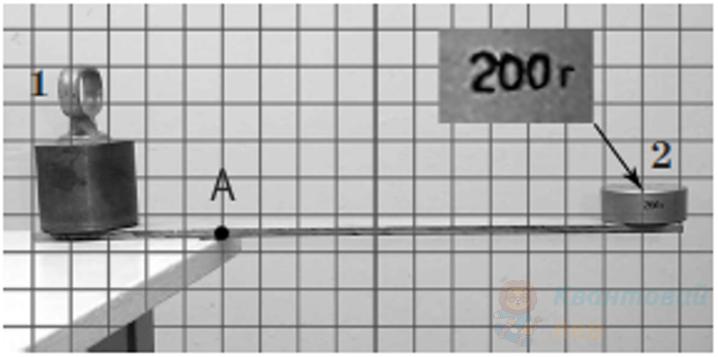
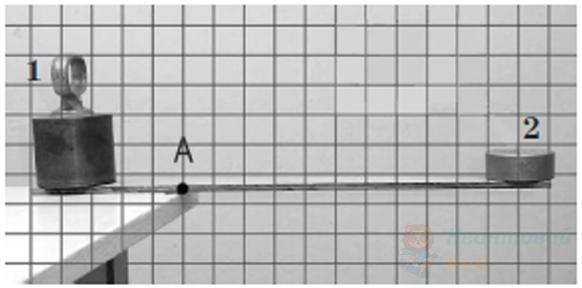
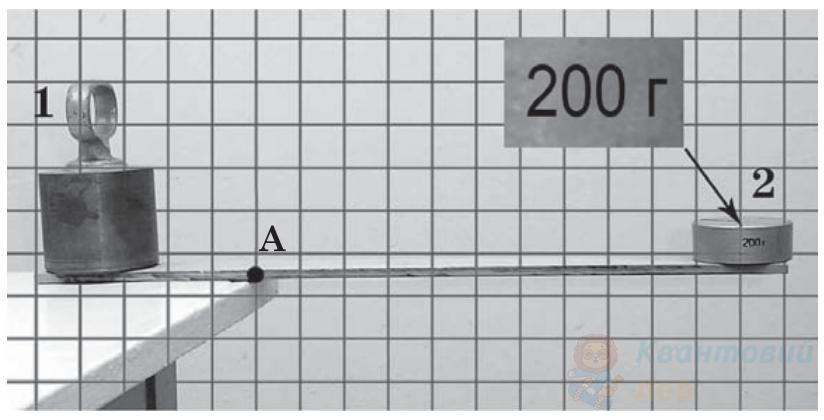
Обчисліть момент сили тяжіння, яка діє на вантаж 2, відносно горизонтальної осі, що проходить через точку $A$. Масою дерев'яної рейки знехтуйте. Період сітки, накладеної на фото, дорівнює $5 \mathrm{~см}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
А
$1 \mathrm{~Н} \cdot \mathrm{м}$
Б
$1,1 \mathrm{~Н} \cdot \mathrm{м}$
Правильна відповідь
В
$1,2 \mathrm{~Н} \cdot \mathrm{м}$
Г
$0 \mathrm{~Н} \cdot \mathrm{м}$
Трактор масою $8 \mathrm{~т}$ рухається по мосту зі швидкістю $36 \mathrm{~км}/\mathrm{год}$. Визначте, яка сила тиску трактора на середину мосту, якщо міст опуклий і має радіус $200 \mathrm{~м}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
В
$76 \mathrm{~кН}$
Правильна відповідь
Обчисліть масу вантажу 2, якщо момент сили тяжіння цього вантажу відносно горизонтальної осі, що проходить через точку $A$ дорівнює $0,55 \mathrm{~H} \cdot \mathrm{м}$. Масою дерев'яної рейки знехтуйте. Період сітки, накладеної на фото, дорівнює $2,5 \mathrm{~см}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
В
$200 \mathrm{~г}$
Правильна відповідь
Трактор рухається по мосту зі швидкістю $36 \mathrm{~км}/\mathrm{год}$. Визначте масу трактора, якщо сила тиску трактора на середину опуклого мосту радіусом $200 \mathrm{~м}$ дорівнює $76 \mathrm{~кН}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
Б
$8 \mathrm{~т}$
Правильна відповідь
На якому рисунку зображено рухомі об’єкти, що НЕ перебувають у стані невагомості?
А
діти підстрибнули
Б
підлітки їдуть у ліфті, який повільно підіймається
Правильна відповідь
В
падають корок, пір'їнка й дріб
Г
космонавт у відкритому космосі
Установіть відповідність між математичним виразом (1-4), який визначає зміст фізичної величини, та назвою приладу (А – Д), за допомогою якого вимірюють цю величину.
Позначення: $s$ – шлях, $t$ – час, $\rho$ – густина, $g$ – прискорення вільного падіння, $h$ – висота стовпчика рідини, $\rho_{\text{н}}$ – густина насиченої пари, $m$ – маса.
Варіанти зліва
3
$\frac{\rho}{\rho_{\text{н}}} \cdot 100 \%$
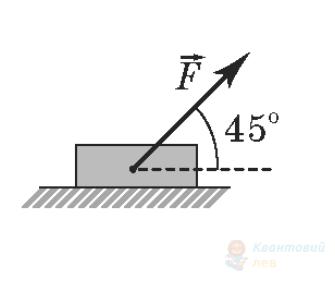
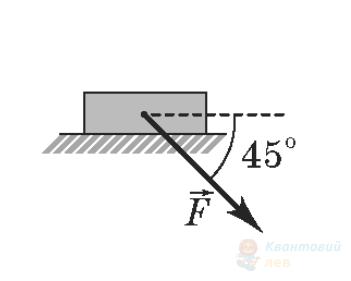
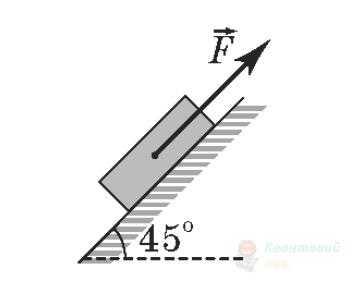
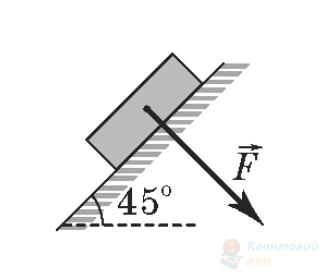
До тіла масою $m$ прикладено силу $F$, як зображено на рисунках. Установіть відповідність між рисунком і виразом для модуля сили реакції опори. Вважайте, що в усіх випадках для модулів сил виконується співвідношення $mg > \sqrt{2} F$.
Варіанти справа
А
$\frac{\sqrt{2}}{2} m g – F$
Б
$\frac{\sqrt{2}}{2} m g + F$
Г
$m g – \frac{\sqrt{2}}{2} F$
Д
$m g + \frac{\sqrt{2}}{2} F$
У ліфті встановлено пружинні терези, на них підвішено тіло масою $1 \mathrm{~кг}$. Установіть відповідність між напрямком та модулем прискорення руху ліфта і показами терезів. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
Варіанти зліва
1
починає підійматися з прискоренням $5 \mathrm{~м} / \mathrm{с}^{2}$
2
рухається вгору сповільнено із прискоренням $5 \mathrm{~м} / \mathrm{с}^{2}$
3
починає спускатися з прискоренням $2,5 \mathrm{~м} / \mathrm{с}^{2}$
4
рухається вниз сповільнено із прискоренням $3,5 \mathrm{~м} / \mathrm{с}^{2}$
Установіть відповідність між назвами сил та їхнім аналітичним записом (формулою):
Варіанти справа
Б
$F=G \frac{m_{1} \cdot m_{2}}{R^{2}}$
Установіть відповідність між станом тіла масою $5 \mathrm{~кг}$ та його вагою. Уважайте, що прискорення вільного падіння на Землі становить $10 \mathrm{~м} / \mathrm{с}^{2}$, на Місяці – $1,6 \mathrm{~м} / \mathrm{с}^{2}$.
Варіанти зліва
1
тіло у швидкісному ліфті, що рухається вниз із прискоренням $2 \mathrm{~м} / \mathrm{с}^{2}$
2
тіло вільно падає біля поверхні Землі
3
тіло зважують на поверхні Місяця
4
тіло в міжпланетному кораблі, який робить маневр із прискоренням $6 \mathrm{~м} / \mathrm{с}^{2}$
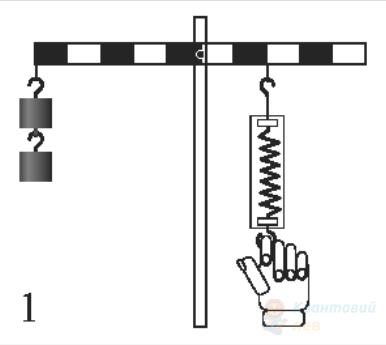
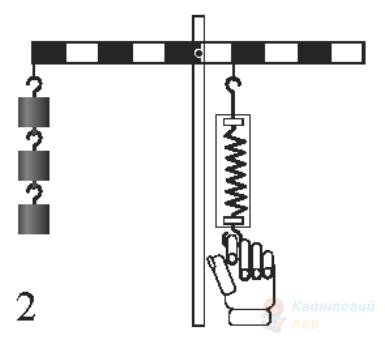
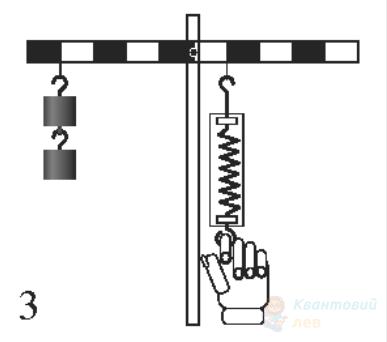
Важелі, зображені на рисунках, знаходяться у рівновазі. Кожен тягарець має масу $100 \mathrm{~г}$. Установіть відповідність між цими рисунками і показами динамометрів. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$
До початку речення (А-Д) доберіть його закінчення (1-4) так, щоб утворилося правильне твердження.
Варіанти зліва
4
не змінюється (не дорівнює нулю).
Варіанти справа
А
Зі збільшенням кута нахилу похилої площини сила тертя спокою, яка діє на нерухоме тіло, ...
Б
Робота сили тяжіння, яка діє на автомобіль, що рухається горизонтальною дорогою, ...
В
Під час руху Землі навколо Сонця по траєкторії, яку вважаємо колом, модуль сили їхньої взаємодії ...
Г
Сила пружності, яка діє з боку рейок на бокову поверхню коліс, коли швидкість руху поїзда на повороті стає меншою, ...
Д
Сила натягу нитки за час одного повного коливання на ній кульки ...
Узгодьте фізичне явище (1-4) з його причиною (А-Д).
Варіанти зліва
2
виникнення архімедової сили
Варіанти справа
А
залежність сил тяжіння від відстані
Б
залежність тиску рідини від глибини
В
однакові прискорення тіла і його опори під час вільного падіння
Г
взаємодія молекул рідини й твердого тіла
Д
залежність тиску рідини від її густини
Визначте максимальну масу вантажу, який можна перевезти через річку на плоту, складеному з 10 соснових колод об'ємом $0,5 \mathrm{~м}^{3}$ кожна. Уважайте, що густина соснової деревини дорівнює $600 \mathrm{~кг} / \mathrm{м}^{3}$, води – $1000 \mathrm{~кг} / \mathrm{м}^{3}$, а прискорення вільного падіння становить $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у кілограмах ($\mathrm{кг}$).
Правильна відповідь:
2000.0
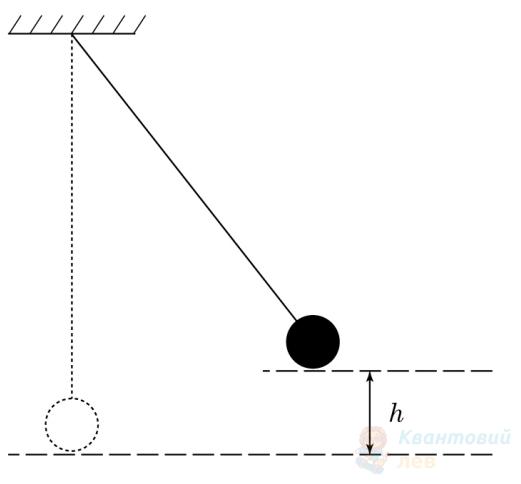
Маленька кулька масою $0,1 \mathrm{~кг}$ гойдається на нерозтяжній невагомій нитці завдовжки $1 \mathrm{~м}$ (див. рисунок). У момент проходження кулькою положення рівноваги сила натягу нитки становить $1,5 \mathrm{~Н}$. Визначте, до якої максимальної висоти $h$ відносно положення рівноваги підіймається кулька. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Правильна відповідь:
0.25
Тягарець висить на пружині жорсткістю $200 \mathrm{~H} / \mathrm{м}$. Визначте масу тягарця, якщо під його дією пружина розтягнулася на $1,5 \mathrm{~см}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Відповідь запишіть у кілограмах ($\mathrm{кг}$).
Вертикально розташований дріт радіусом $0,5 \mathrm{~мм}$ опустили в мильний розчин і повільно підняли. Визначте масу краплі, що відривається після цього від дроту. Уважайте, що поверхневий натяг мильного розчину дорівнює $0,04 \mathrm{~Н} / \mathrm{м}$, прискорення вільного падіння становить $10 \mathrm{~м} / \mathrm{с}^{2}, \pi=3,14$. Відповідь запишіть у міліграмах ($\mathrm{мг}$).
Правильна відповідь:
12.56
Горизонтальний провідний стержень масою $20 \mathrm{~г}$ підвішено за кінці на двох легких дротах. Середня частина стержня довжиною $30 \mathrm{~см}$ перебуває в однорідному магнітному полі. Магнітна індукція поля напрямлена горизонтально під прямим кутом до провідника, їі модуль дорівнює $0,2 \mathrm{~Тл}$. Коли стержнем пропустили струм, сили натягу дротів збільшилися. Визначте, якою стала сила натягу кожного дроту. Сила струму дорівнює $5 \mathrm{~А}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у ньютонах ($\mathrm{H}$).
Правильна відповідь:
0.25
Унаслідок ожеледиці коефіцієнт тертя між шинами та поверхнею шосе зменшився від $0,72$ до $0,18$. Визначте, у скільки разів зменшилася максимально можлива швидкість руху на поворотах. Поверхню шосе вважайте горизонтальною.
Визначте масу бруска, що висить на нитці (див. рисунок). Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у грамах ($\mathrm{г}$).
Правильна відповідь:
90.0
Із якою швидкістю гойдалка проходить нижню точку, якщо вага дитини масою $40 \mathrm{~кг}$ у цій точці становить $800 \mathrm{~Н}$ ? Довжина підвісу гойдалки дорівнює $2,5 \mathrm{~м}$. Уважайте, що прискорення вільного падіння становить $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у метрах за секунду ($\mathrm{м} / \mathrm{с}$).
Бетонний циліндричний стовп, що лежав на горизонтальному дні глибокого озера, водолази поставили вертикально. Висота стовпа $4 \mathrm{~м}$, маса $600 \mathrm{~кг}$. Визначте мінімальну роботу, яку мали виконати водолази, піднявши стовп. Уважайте, що густина бетону $2000 \mathrm{~кг} / \mathrm{м}^{3}$, густина води $1000 \mathrm{~кг} / \mathrm{м}^{3}$, прискорення вільного падіння $10 \mathrm{~м} / \mathrm{с}^{2}$. Поперечні розміри стовпа не враховуйте.
Відповідь запишіть у кілоджоулях ($\mathrm{кДж}$).
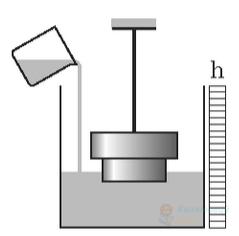
На цифрових терезах, які відображають результат зважування в грамах, виконали кілька зважувань. Спочатку зважили склянку з водою (фото 1). Потім у склянку занурили металевий брусок на нитці так, щоб він не торкався дна та стінок, і знову зважили склянку (фото 2). Для третього зважування нитку відпустили так, щоби брусок ліг на дно склянки (фото 3). Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$, густина води становить $1000 \mathrm{~кг} / \mathrm{м}^{3}$. Брусок в обох випадках занурений у воду повністю.
Визначте виштовхувальну силу, що діє на брусок.
Відповідь запишіть у ньютонах ($\mathrm{H}$).
Правильна відповідь:
0.12
Якщо вантаж $t$ невідомої маси підвісити до короткого плеча важеля, то його можна зрівноважити вантажем масою $400 \mathrm{~г}$. Якщо вантаж $t$ підвісити до довгого плеча важеля, не змінюючи положення точки опори $O$, то його можна зрівноважити вантажем масою $900 \mathrm{~г}$. Масою важеля знехтуйте.
Визначте відношення довжини більшого плеча важеля до меншого.
Якщо вантаж $t$ невідомої маси підвісити до короткого плеча важеля, то його можна зрівноважити вантажем масою $400 \mathrm{~г}$. Якщо вантаж $t$ підвісити до довгого плеча важеля, не змінюючи положення точки опори $O$, то його можна зрівноважити вантажем масою $900 \mathrm{~г}$. Масою важеля знехтуйте.
Яка маса $m$ вантажу?
Відповідь запишіть у грамах ($\mathrm{г}$)
Правильна відповідь:
600.0
Визначте модуль моменту сили тяжіння, яка діє на вантаж 2, відносно горизонтальної осі, що проходить через точку А перпендикулярно до рейки. Період сітки, накладеної на фото, дорівнює $5 \mathrm{~см}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у ньютон-метрах ($\mathrm{Н} \cdot \mathrm{м}$)
Автомобіль масою $3 \mathrm{~т}$ рухається рівномірно прямолінійно зі швидкістю $72 \mathrm{~км}/\mathrm{год}$, коефіцієнт опору дорівнює $0,06$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Яку потужність розвиває двигун автомобіля?
Відповідь запишіть у кіловатах (кВт).
Правильна відповідь:
36.0
Автомобіль масою $3 \mathrm{~т}$ рухається рівномірно прямолінійно зі швидкістю $72 \mathrm{~км}/\mathrm{год}$, коефіцієнт опору дорівнює $0,06$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Яку роботу виконує двигун автомобіля на кожному кілометрі дороги?
Відповідь запишіть у мегаджоулях (МДж).
Космічний апарат спустився на поверхню планети $Z$, радіус якої у 2 рази більший за радіус Землі, а середня густина планети $Z$ у 4 рази менша за середню густину Землі. Яка сила тяжіння діє на апарат на поверхні планети $Z$, якщо на поверхні Землі на нього діяла би сила тяжіння $1600 \mathrm{~Н}$?
Відповідь запишіть у ньютонах ($\mathrm{Н}$).
Правильна відповідь:
800.0
Кільце радіусом $5 \mathrm{~см}$, виготовлене з тонкого дроту, потрібно відірвати від поверхні води. Маса кільця $1,2 \mathrm{~г}$, поверхневий натяг води $70 \mathrm{~мН} / \mathrm{м}$. Визначте силу, яку потрібно докласти до кільця. Уважайте, що під час відриву від води кільце лишається горизонтальним, прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}, \pi=\frac{22}{7}$.
Відповідь запишіть у міліньютонах ($\mathrm{мН}$).
Правильна відповідь:
56.0
Дерев'яна дошка завтовшки $40 \mathrm{~мм}$ плаває у воді. Нижня поверхня дошки перебуває на глибині $30 \mathrm{~мм}$. Уважайте, що густина води дорівнює $1000 \mathrm{~кг} / \mathrm{м}^{3}$. Визначте, якою є густина деревини.
Відповідь запишіть у кілограмах на метр кубічний ($\mathrm{кг} / \mathrm{м}^{3}$).
Правильна відповідь:
750.0
Край дошки підняли на $1,5 \mathrm{~м}$ над підлогою. Яку найменшу швидкість необхідно надати невеликому тілу в нижній точці дошки, щоб воно, ковзаючи по ній, змогло досягти верхньої точки? Довжина дошки – $2,5 \mathrm{~м}$, коефіцієнт тертя ковзання становить 0,15 ; прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Відповідь запишіть у метрах на секунду ($\mathrm{м} / \mathrm{с}$)
Аеростат масою $250 \mathrm{~кг}$ почав опускатися з прискоренням $0,2 \mathrm{~м} / \mathrm{с}^{2}$. Визначте масу баласту, який потрібно скинути за борт, щоб аеростат почав рухатися вгору з таким самим прискоренням. Опір повітря не враховуйте. Уважайте, що прискорення вільного падіння дорівнює $9,8 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у кілограмах ($\mathrm{кг}$)
Правильна відповідь:
10.0
Дерев'яний брусок плаває у воді, занурившись на $10 \mathrm{~см}$. Якщо знизу до бруска прикріпити вантаж певної маси, то брусок зануриться у воду на глибину $14 \mathrm{~см}$. На скільки брусок буде занурений у воду, якщо цей вантаж покласти на нього зверху? Густина матеріалу вантажу дорівнює $5000 \mathrm{кг} / \mathrm{м}^{3}$, густина води – 1000 кг/м$^{3}$. У всіх випадках (див. схематичний рисунок) брусок не нахиляється, не перевертається, вода не покриває верхню грань бруска.
Відповідь запишіть у сантиметрах ($\mathrm{см}$)
Правильна відповідь:
15.0
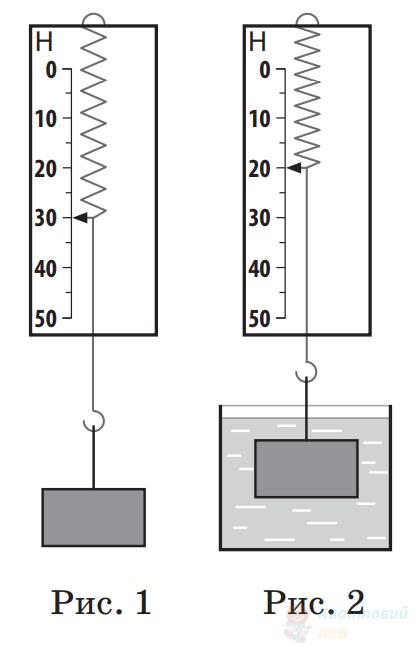
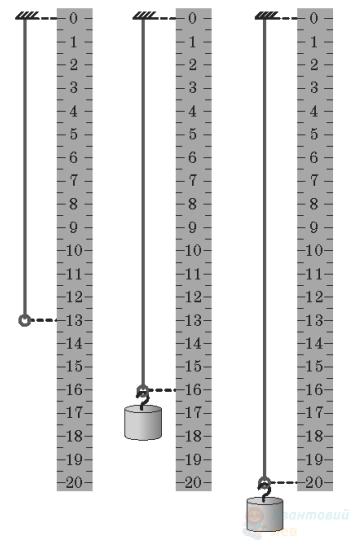
На рисунку зображено динамометр із причепленим до нього тілом у повітрі (рис. 1) та в рідині (рис. 2). Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Визначте масу тіла.
Відповідь запишіть у кілограмах ($\mathrm{кг}$)
Похила площина утворює кут із горизонтом. Тіло, яке поклали на площину, зісковзує вниз із прискоренням $2 \mathrm{~м} / \mathrm{с}^{2}$. Визначте коефіцієнт тертя ковзання. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Усі білі й сірі важки, з яких складено вантажі (див. фото), мають однакову масу. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Тертям у блоці й масою нитки знехтуйте.
Обчисліть модуль прискорення, з яким рухатиметься система, зображена на фотографії, якщо прибрати підставку з-під лівого вантажу.
Відповідь запишіть у метрах за секунду в квадраті ($\mathrm{м} / \mathrm{с}^{2}$).
Усі білі й сірі важки, з яких складено вантажі (див. фото), мають однакову масу. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Тертям у блоці й масою нитки знехтуйте.
Визначте силу натягу нитки, до якої підвішено вантажі. Маса кожного важка дорівнює $100 \mathrm{~г}$.
Відповідь запишіть у ньютонах ($\mathrm{Н}$).
Правильна відповідь:
3.75
Визначте, яку роботу виконує людина під час повільного піднімання на $60 \mathrm{~см}$ під водою каменя масою $50 \mathrm{~кг}$ і об'ємом $0,02 \mathrm{~м}^{3}$. Густина води дорівнює $10^{3} \mathrm{~кг} / \mathrm{м}^{3}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у джоулях ($\mathrm{Дж}$).
Правильна відповідь:
180.0
Два стержні жорстко з'єднані, як показано на рисунку, і прикріплені до стіни. До них прикріплено вантаж масою $2,5 \mathrm{~кг}$. $A B=5 \mathrm{~см}, A C=3 \mathrm{~см}, B C=4 \mathrm{~см}$. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$, а стержні невагомі.
Визначте силу пружності в стержні $B C$.
Правильна відповідь:
20.0
Під час повільного підйому корабельного якоря об'ємом $0,2 \mathrm{~м}^{3}$ у воді було виконано роботу $26 \mathrm{~кДж}$. Густина металу якоря дорівнює $7500 \mathrm{~кг} / \mathrm{м}^{3}$, густина води – $1000 \mathrm{~кг} / \mathrm{м}^{3}$. Визначте висоту, на яку у воді підняли якір. Опором води знехтуйте. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у метрах ($\mathrm{м}$)
Два стержні жорстко з'єднані, як показано на рисунку, і прикріплені до стіни. До них прикріплено вантаж масою $2,5 \mathrm{~кг}$. $A B=5 \mathrm{~см}, A C=3 \mathrm{~см}, B C=4 \mathrm{~см}$. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$, а стержні невагомі.
Визначте силу пружності в стержні $A C$.
Правильна відповідь:
15.0
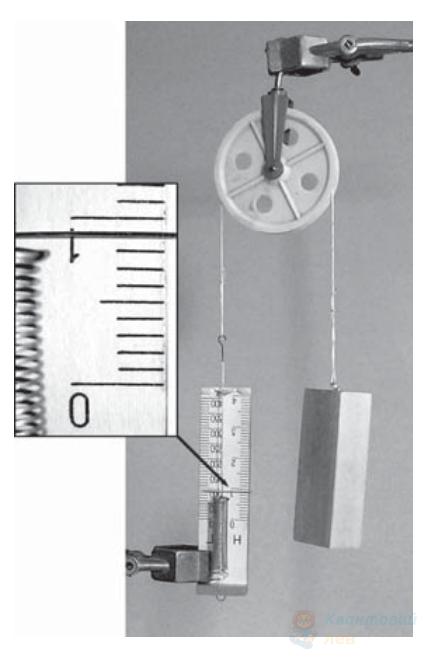
Тягарець, підвішений до гумової стрічки, здійснює вертикальні коливання. На рисунку поруч з лінійкою зображено гумову стрічку без тягарця і крайні відхилення тягарця від положення рівноваги в процесі коливань. Визначте максимальну швидкість тягарця під час таких коливань. Вважайте, що для гумової стрічки виконується закон Гука; $g=9,8 \mathrm{~м} / \mathrm{с}^{2}$. Ціна поділки лінійки становить $0,5 \mathrm{~см}$.
Відповідь запишіть у $\mathrm{см} / \mathrm{с}$.
Правильна відповідь:
28.0
Щоб відірвати від поверхні рідини тонку горизонтальну дротинку довжиною $8 \mathrm{~см}$ і масою $0,48 \mathrm{~г}$, до неї необхідно прикласти силу $12 \mathrm{~мН}$, напрямлену вертикально вгору. Визначте поверхневий натяг рідини, уважаючи, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$. Відповідь запишіть у міліньютонах на метр.
Правильна відповідь:
45.0
Порожниста скляна куля плаває, повністю занурившись у воду. Визначте, яку частину об'єму кулі займає порожнина. Густина води дорівнює 1000 кг/м³, а густина скла – 2500 кг/м³.
Повітряну кулю заповнено газом, густина якого в 6 разів менша за густину повітря. У скільки разів збільшиться допустима маса вантажу, який може підняти куля, якщо газ у ній підігріли, унаслідок чого його густина зменшилася ще удвічі? Вагою оболонки кулі знехтуйте.
Дві однакові кульки підвішені на нерозтяжних і невагомих нитках однакової довжини. Після того як кулькам надали однаковий заряд, нитки з кульками розійшлися на певний кут. Після цього кульки опустили в гас, густина якого становить $800 \mathrm{~кг}/\mathrm{м}^{3}$, а діелектрична проникність гасу дорівнює 2. Визначте густину матеріалу кульки (у $\mathrm{кг}/\mathrm{м}^{3}$), якщо в гасі кут між нитками не змінився.
Правильна відповідь:
1600.0
Трамвай масою $25 \mathrm{~т}$ рівномірно рухається по горизонтальній прямолінійній ділянці шляху зі швидкістю $36 \mathrm{~км}/\mathrm{год}$. Напруга живлення двигуна дорівнює $550 \mathrm{~В}$, сила струму у двигуні становить $400 \mathrm{~А}$. Сила опору рухові становить $0,055$ ваги трамваю. Визначте коефіцієнт корисної дії (ККД) використання електроенергії. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$. Відповідь запишіть у відсотках.
Правильна відповідь:
62.5
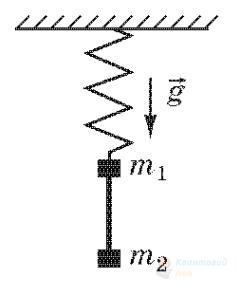
До нижнього кінця легкої пружини підвішені зв’язані невагомою ниткою важки: верхній масою $m_{1}=0,6 \mathrm{~кг}$ і нижній масою $m_{2}=0,3 \mathrm{~кг}$ (див. рисунок). Нитку, що з'єднує важки, перепалюють. Визначте модуль прискорення (у $\mathrm{м} / \mathrm{с}^{2}$), з яким почне рухатися верхній важок. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Тіло масою $2 \mathrm{~кг}$ ковзає вниз по площині, нахиленій під кутом $45^{\circ}$ до горизонту. Висота площини становить $50 \mathrm{~см}$, коефіцієнт тертя ковзання – 0,2. На скільки зросте внутрішня енергія (у $\mathrm{Дж}$) тіла й похилої площини при зісковзуванні тіла від верхньої точки площини до її основи? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Брусок перебуває на горизонтальній дошці завдовжки $2 \mathrm{~м}$. Коефіцієнт тертя між бруском і дошкою дорівнює $\frac{3}{4}$. На яку мінімальну висоту треба підняти один край дошки, щоб брусок міг зісковзувати по ній?
Відповідь запишіть у метрах.
Повітряна куля з газонепроникною оболонкою масою $400 \mathrm{~кг}$ заповнена гелієм. Куля може нерухомо утримувати вантаж масою $225 \mathrm{~кг}$ у повітрі на певній висоті. Визначте масу гелію в кулі. Вважайте, що об'єм вантажу малий, а оболонка кулі не спричиняє опору зміні об'єму кулі і є тонкою. Молярна маса гелію дорівнює $4 \cdot 10^{-3} \mathrm{~кг} / \mathrm{моль}$. Повітря вважайте газом з молярною масою $29 \cdot 10^{-3} \mathrm{~кг} / \mathrm{моль}$. Гелій і повітря вважайте ідеальними газами. Відповідь запишіть у кілограмах.
Правильна відповідь:
100.0
Магніт масою $500 \mathrm{~г}$ прилип до вертикальної залізної стінки. Під дією вертикальної сили $0,2 \mathrm{~Н}$ магніт рівномірно рухається вниз. Під дією якої вертикальної сили магніт почне рівномірно рухатися вгору? Вважайте, що $g=9,8 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у ньютонах.
Правильна відповідь:
10.0
Підйомник гірськолижного курорту піднімає 45 лижників на висоту $2 \mathrm{~км}$ за $20 \mathrm{~хв}$. Уважайте, що середня маса одного лижника дорівнює $70 \mathrm{~кг}$, а прискорення вільного падіння $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Обчисліть корисну роботу (МДж), яку виконує підйомник.
Правильна відповідь:
63.0
Важіль 1 без тертя може вільно обертатися навколо осі 2, як зображено на рисунку. Спочатку без важків та вантажу 3 важіль було зрівноважено. Визначте масу вантажу 3.
Відповідь запишіть у кілограмах ($\mathrm{кг}$).
Гумова нитка площею перерізу $1{,}5\mathrm{~мм}^2$ і $60\mathrm{~см}$ завдовжки під дією тягарця масою $100\mathrm{~г}$ видовжилася на $2\mathrm{~см}$. Обчисліть значення модуля Юнга для гуми.
Вважайте, що прискорення вільного падіння дорівнює $10\mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у мегапаскалях ($\mathrm{МПа}$).
Правильна відповідь:
20.0
Під час вільного падіння імпульс м’яча збільшився на $12 \mathrm{~кг} \cdot \mathrm{м} / \mathrm{с}$ за $2$ секунди. Обчисліть масу м'яча. Вважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Відповідь запишіть у кілограмах ($\mathrm{кг}$).
