Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
Тіло рівномірно зісковзує з похилої площини. Визначте, які співвідношення правильні для роботи сили тяжіння $A_{\text{тяж}}$ і роботи сили тертя $A_{\text{тер}}$ (силу опору повітря не враховуйте).
А
$A_{\text{тяж}}=A_{\text{тер}}=0$
Б
$A_{\text{тяж}}=A_{\text{тер}}>0$
В
$A_{\text{тяж}}=-A_{\text{тер}}>0$
Правильна відповідь
Г
$A_{\text{тяж}}=-A_{\text{тер}}<0$
Дерев'яний брусок рівномірно ковзає вниз похилою площиною (див. рисунок). Визначте коефіцієнт тертя ковзання бруска похилою площиною.
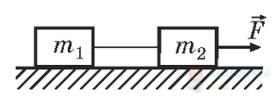
На столі знаходяться два бруски масами $m_{1} = 1 \mathrm{~кг}$ і $m_{2} = 2 \mathrm{~кг}$, зв'язані невагомою нерозтяжною ниткою (див. рисунок). Коефіцієнти тертя між брусками та столом відповідно дорівнюють $\mu_{1}=0,5$ і $\mu_{2}=0,3$. До другого бруска прикладають горизонтальну силу $\vec{F}$, модуль якої дорівнює $8 \mathrm{~Н}$ . Визначте силу натягу нитки. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
А
$2 \mathrm{~Н}$
Правильна відповідь
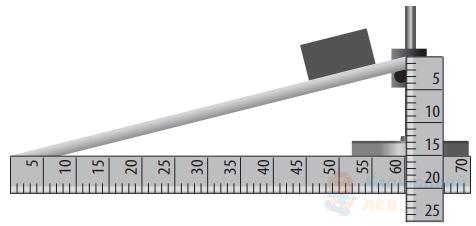
Спочатку брусок, навантажений тягарцями, рівномірно тягли по горизонтальній рейці (див. фото 1). Потім цей брусок разом з тягарцями зважили (див. фото 2). Визначте за результатами вимірювань коефіцієнт тертя між бруском і рейкою.
Установіть відповідність між процесом (1-4) та формулою (А – Д), що його описує.
Позначення: $A$ – робота, $m$ – маса, $g$ – прискорення вільного падіння, $h$ – висота, $E$ – енергія, $k$ – коефіцієнт жорсткості, $x$ – видовження, $F$ – сила, $\mu$ – коефіцієнт тертя, $N$ – сила реакції опори, $l$ – плече, $\rho$ – густина, $V$ – об'єм.
Варіанти зліва
1
розтягування гумової нитки
3
ковзання черевика по підлозі
4
плавання м'яча на поверхні озера
Варіанти справа
Г
$F_{1} l_{1}=F_{2} l_{2}$
Д
$F=\rho_{\text{рідини}} g V$
Установіть відповідність між процесом (1-4) та формулою (А-Д), що його описує.
Варіанти зліва
1
відро з водою утримується за допомогою колодязного «журавля»
3
автомобіль досягає своєї максимальної швидкості
4
деталі механізмів змащують мастилом
Варіанти справа
А
$F_{1} l_{1}=F_{2} l_{2}$
Д
$T=2 \pi \sqrt{\frac{l}{g}}$
Установіть відповідність між процесом (1-4) та формулою (А-Д), що його описує.
Варіанти зліва
1
взаємодіють Венера і Марс
2
розтягується гумова нитка
3
стрічка транспортера пересуває цеглину, яка лежить на ній
4
маленька сталева кулька коливається на довгій нерозтяжній нитці
Варіанти справа
А
$F=G \frac{m_{1} \cdot m_{2}}{R^{2}}$
Б
$T=2 \pi \sqrt{\frac{l}{g}}$
Установіть відповідність між назвами сил та їхнім аналітичним записом (формулою).
Варіанти справа
Д
$F=\rho_{\text{рідини}} g V$
Установіть відповідність між процесами та формулами, що їх описують.
Варіанти зліва
1
Розтягується гумова нитка.
3
Черевик ковзає по підлозі.
4
М'яч плаває на поверхні озера.
Варіанти справа
Г
$F_{1} l_{1}=F_{2} l_{2}$
Установіть відповідність між назвами сил та їхнім аналітичним записом (формулою):
Варіанти справа
Б
$F=G \frac{m_{1} \cdot m_{2}}{R^{2}}$
Установіть відповідність між назвами сил та їхнім аналітичним записом (формулою):
Варіанти справа
Г
$F=G \frac{m_{1} m_{2}}{R^{2}}$;
Унаслідок ожеледиці коефіцієнт тертя між шинами та поверхнею шосе зменшився від $0,72$ до $0,18$. Визначте, у скільки разів зменшилася максимально можлива швидкість руху на поворотах. Поверхню шосе вважайте горизонтальною.
Автомобіль масою $3 \mathrm{~т}$ рухається рівномірно прямолінійно зі швидкістю $72 \mathrm{~км}/\mathrm{год}$, коефіцієнт опору дорівнює $0,06$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Яку потужність розвиває двигун автомобіля?
Відповідь запишіть у кіловатах (кВт).
Правильна відповідь:
36.0
Автомобіль масою $3 \mathrm{~т}$ рухається рівномірно прямолінійно зі швидкістю $72 \mathrm{~км}/\mathrm{год}$, коефіцієнт опору дорівнює $0,06$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Яку роботу виконує двигун автомобіля на кожному кілометрі дороги?
Відповідь запишіть у мегаджоулях (МДж).
Край дошки підняли на $1,5 \mathrm{~м}$ над підлогою. Яку найменшу швидкість необхідно надати невеликому тілу в нижній точці дошки, щоб воно, ковзаючи по ній, змогло досягти верхньої точки? Довжина дошки – $2,5 \mathrm{~м}$, коефіцієнт тертя ковзання становить 0,15 ; прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Відповідь запишіть у метрах на секунду ($\mathrm{м} / \mathrm{с}$)
Похила площина утворює кут із горизонтом. Тіло, яке поклали на площину, зісковзує вниз із прискоренням $2 \mathrm{~м} / \mathrm{с}^{2}$. Визначте коефіцієнт тертя ковзання. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Тіло масою $2 \mathrm{~кг}$ ковзає вниз по площині, нахиленій під кутом $45^{\circ}$ до горизонту. Висота площини становить $50 \mathrm{~см}$, коефіцієнт тертя ковзання – 0,2. На скільки зросте внутрішня енергія (у $\mathrm{Дж}$) тіла й похилої площини при зісковзуванні тіла від верхньої точки площини до її основи? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Брусок перебуває на горизонтальній дошці завдовжки $2 \mathrm{~м}$. Коефіцієнт тертя між бруском і дошкою дорівнює $\frac{3}{4}$. На яку мінімальну висоту треба підняти один край дошки, щоб брусок міг зісковзувати по ній?
Відповідь запишіть у метрах.
Магніт масою $500 \mathrm{~г}$ прилип до вертикальної залізної стінки. Під дією вертикальної сили $0,2 \mathrm{~Н}$ магніт рівномірно рухається вниз. Під дією якої вертикальної сили магніт почне рівномірно рухатися вгору? Вважайте, що $g=9,8 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у ньютонах.
Правильна відповідь:
10.0