Архів завдань ЗНО та НМТ з фізики Teacher Edition
Інтерактивна база офіційних завдань ЗНО та НМТ з фізики — для викладачів та учнів

Інтерактивна база офіційних завдань ЗНО та НМТ з фізики — для викладачів та учнів
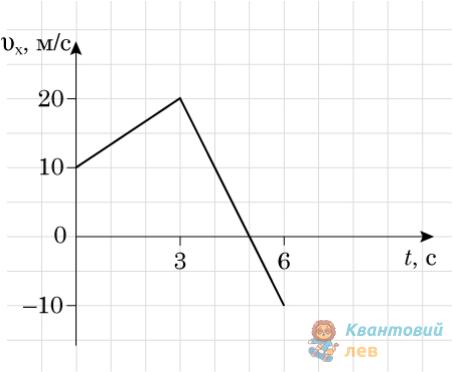
Шлях при рівноприскореному русі