Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
Парашутист опускається рівномірно зі швидкістю $5 \mathrm{~м}/\mathrm{с}$. На відстані $100 \mathrm{~м}$ від поверхні землі з його кишені випала монета. На скільки секунд пізніше приземлиться парашутист, ніж впаде монета? Вплив опору повітря на монету не враховувати. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$16 \mathrm{~с}$
Правильна відповідь
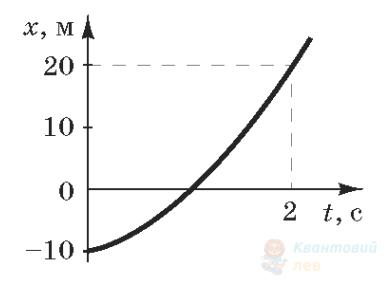
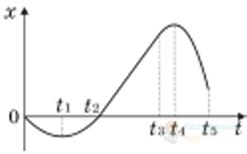
На рисунку зображено графік залежності координати $x$ матеріальної точки, що рухається рівноприскорено вздовж осі $O x$, від часу $t$. Визначте модуль прискорення даної точки, якщо в момент початку відліку часу модуль її швидкості дорівнював $3 \mathrm{~м} / \mathrm{с}$.
А
$2 \mathrm{~м} / \mathrm{с}^{2}$
Б
$4 \mathrm{~м} / \mathrm{с}^{2}$
В
$12 \mathrm{~м} / \mathrm{с}^{2}$
Правильна відповідь
Г
$24 \mathrm{~м} / \mathrm{с}^{2}$
Визначте, яка залежність координати тіла $x$ від часу $t$ описує прямолінійний рівноприскорений рух уздовж осі $O x$ з початковою швидкістю $6 \mathrm{~м}/\mathrm{с}$ та прискоренням $1 \mathrm{~м}/ \mathrm{с}^{2}$. Усі величини у формулах виражено в одиницях SI.
В
$x=1+6 t+0,5 t^{2}$
Правильна відповідь
Визначте масу вантажу, підвішеного до блока. Масою блока знехтуйте. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$10 \mathrm{~кг}$
Правильна відповідь
Кулька без початкової швидкості скотилася з похилого жолоба завдовжки $0,72 \mathrm{~м}$. Знайдіть прискорення, з яким рухалася кулька. Покази секундоміра (див. фото 1 і 2) означають хвилини, секунди та соті частки секунди на початку та в кінці руху кульки відповідно.
А
$0,6 \mathrm{~м} / \mathrm{с}^{2}$
Б
$0,72 \mathrm{~м} / \mathrm{с}^{2}$
В
$1 \mathrm{~м} / \mathrm{с}^{2}$
Правильна відповідь
Г
$1,2 \mathrm{~м} / \mathrm{с}^{2}$
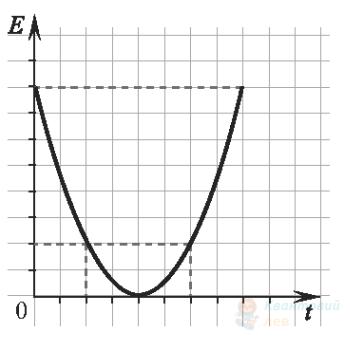
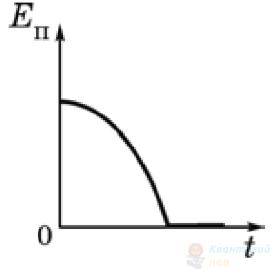
Камінець кинули вертикально вгору. Правильно закінчить речення: графік, зображений на рисунку, може відповідати
А
залежності кінетичної енергії камінця від часу.
Б
залежності потенціальної енергії камінця від часу.
В
залежності різниці між потенціальною і кінетичною енергією камінця від часу.
Г
залежності повної механічної енергії камінця від часу.
Правильна відповідь
3 даху будівлі висотою $4,9 \mathrm{~м}$ впала крижинка. Визначте швидкість падіння крижинки в момент досягнення нею землі. Опором повітря знехтуйте. Вважайте, що $g=9,8 \mathrm{~м} / \mathrm{с}^{2}$.
А
$1 \mathrm{~м} / \mathrm{с}$
Б
$4,9 \mathrm{~м} / \mathrm{с}$
В
$9,8 \mathrm{~м} / \mathrm{с}$
Правильна відповідь
Г
$18 \mathrm{~м} / \mathrm{с}$
Під час ремонту будинку шматки штукатурки падають з третього поверху. Визначте, з якого поверху шматки штукатурки падають удвічі довше. Висота, з якої падають шматки, визначається кількістю нижніх поверхів під тим, з якого вони впали. Опором повітря знехтуйте.
В
З дев'ятого
Правильна відповідь
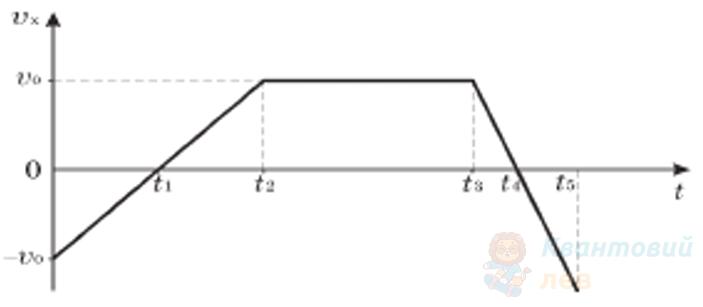
За поданим графіком залежності проєкції швидкості тіла від часу знайдіть графік залежності координати тіла від часу. Початкова координата тіла $x = 0$.
А
 Правильна відповідь
Правильна відповідь
На скільки змістився у вертикальному напрямі електрон, що влетів горизонтально у плоский повітряний конденсатор з горизонтальним розташуванням пластин, на які подана напруга $9 \mathrm{~В}$? Відстань між пластинами конденсатора дорівнює $1 \mathrm{~см}$. Електрон влетів у конденсатор зі швидкістю $10^{7} \mathrm{~м} / \mathrm{с}$ і пролетів у горизонтальному напрямку $10 \mathrm{~см}$. Заряд електрона становить $1,6 \cdot 10^{-19} \mathrm{~Кл}$, маса електрона – $9 \cdot 10^{-31} \mathrm{кг}, g = 10 \mathrm{~м} / \mathrm{с}^{2}$.
Г
$8 \mathrm{~мм}$
Правильна відповідь
Учні на уроці фізкультури грають у волейбол. Визначте максимальну висоту (у метрах) відносно рук гравців, якої досягає м’яч, якщо відомо, що у польоті між двома ударами він перебуває $2 \mathrm{~c}$. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
В
$5 \mathrm{~м}$
Правильна відповідь
Пластилінова кулька вільно падає на підлогу без початкової швидкості. Укажіть графік, що відображає залежність потенціальної енергії цієї кульки від часу.
В
 Правильна відповідь
Правильна відповідь
Вантаж масою $100 \mathrm{~кг}$ тягнуть уздовж горизонтальної поверхні за допомогою мотузки, паралельної площині цієї поверхні. За рівномірного руху вантажу сила натягу, що виникає в мотузці, дорівнює $20 \mathrm{~Н}$. Визначте мінімальний час переміщення цього вантажу зі стану спокою на відстань $5 \mathrm{~м}$, якщо мотузка може витримати максимальну силу натягу $30 \mathrm{~Н}$.
Відповідь запишіть у секундах ($\mathrm{с}$).
Правильна відповідь:
10.0
Тіло вільно падає без початкової швидкості з висоти $5 \mathrm{~м}$. Одночасно з ним починає падати друге тіло, яке кидають вертикально вниз з висоти $10 \mathrm{~м}$. Яка початкова швидкість має бути в другого тіла, щоб обидва тіла впали одночасно? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у метрах на секунду ($\mathrm{м} / \mathrm{с}$).
М'яч підкинули вертикально вгору з початковою швидкістю $20 \mathrm{~м} / \mathrm{с}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Який шлях пройде м'яч до моменту падіння на землю?
Відповідь запишіть у метрах ($ \mathrm{м} $)
Правильна відповідь:
40.0
Тіло вільно падає з висоти $320 \mathrm{~м}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Визначте, скільки часу падатиме тіло.
Відповідь запишіть у секундах ($\mathrm{с}$).
Тіло вільно падає без початкової швидкості. Визначте його модуль переміщення за той проміжок часу, за який швидкість його руху збільшується від 6 до $24 \mathrm{~м}/\mathrm{с}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Відповідь запишіть у метрах.
Правильна відповідь:
27.0
Автомобіль почав рухатися прямолінійно рівноприскорено зі стану спокою і через $5 \mathrm{~c}$ його швидкість дорівнювала $10 \mathrm{~м} / \mathrm{с}$.
Який шлях пройшов автомобіль за $4 \mathrm{~c}$ від початку руху?
Відповідь запишіть у метрах ($\mathrm{м}$)
Правильна відповідь:
16.0
У момент, коли кіт ($К$) помітив мишеня ($M$) (див. рисунок), воно знаходилося на відстані $3 \mathrm{~м}$ від нори $(H)$ і бігло до неї рівномірно зі швидкістю $0,5 \mathrm{~м} / \mathrm{с}$. Наздоганяючи мишеня, кіт почав бігти з постійним прискоренням $2 \mathrm{~м} / \mathrm{с}^{2}$. Уважайте, що кіт і мишеня рухаються по одній прямій, а відстань від кота до нори становить $4,5 \mathrm{~м}$.
На якій відстані ($\mathrm{м}$) від нори кіт упіймає мишеня?
Правильна відповідь:
2.25
Початкова швидкість снаряду, випущеного з гармати вертикально вгору, дорівнює $40 \mathrm{~м} / \mathrm{с}$. У точці максимального підйому снаряд розірвався на два осколки, маси яких відносяться як $1: 5$. Осколок меншої маси полетів горизонтально зі швидкістю $20 \mathrm{~м} / \mathrm{с}$. На якій відстані (у метрах) від точки пострілу впаде осколок більшої маси? Вважайте поверхню Землі плоскою та горизонтальною; $g=10 \mathrm{~м} / \mathrm{с}^{2}$. Опором повітря знехтуйте.
Правильна відповідь:
16.0
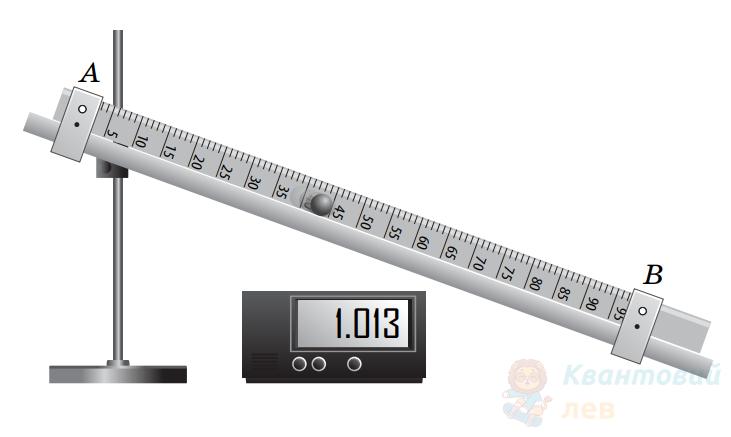
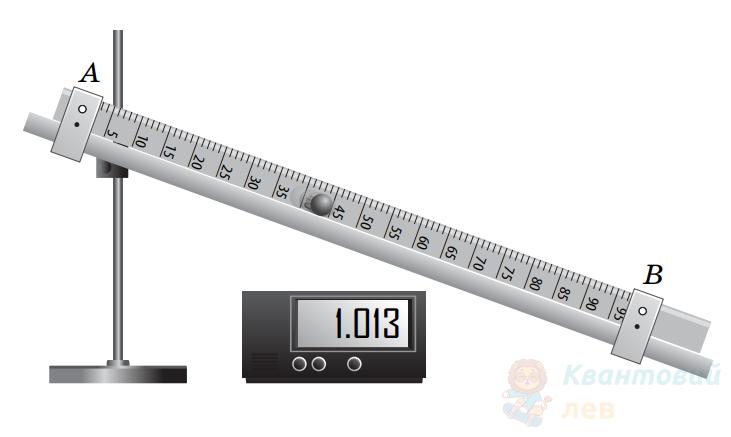
Кулька вільно скочується похилою площиною $A B$, довжина якої 1 метр. Початкова швидкість кульки дорівнює нулю. Провівши 5 експериментів, учень визначив час, за який кулька проходить відстань $A B: t_{1}=0,993 \mathrm{~с} ; t_{2}=0,995 \mathrm{~с}$; $t_{3}=0,987 \mathrm{~с} ; t_{4}=1,012 \mathrm{~с} ; t_{5}=1,013 \mathrm{~с}$.
Визначте швидкість ($\mathrm{м} / \mathrm{с}$), якої набула кулька в точці $В$.
Камінець кинули горизонтально з високої скелі зі швидкістю $7,5 \mathrm{~м}/\mathrm{с}$. Визначте модуль переміщення камінця за $2 \mathrm{~c}$. Опір повітря не враховуйте. Уважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у метрах.
Правильна відповідь:
25.0
Невеличке тіло ковзає зі швидкістю $8 \mathrm{~м}/\mathrm{с}$ по горизонтальній площині, наближаючись до щілини. Щілина утворена двома вертикальними паралельними стінками, розташованими на відстані $0,4 \mathrm{~м}$ одна від одної. Напрямок швидкості руху тіла, що ковзає, перпендикулярний до стінок, які утворюють щілину. Тіло падає на дно щілини глибиною $20 \mathrm{~м}$. Прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$. Визначте кількість ударів тіла об стінки щілини, доки воно досягне дна. Удари тіла об стінки щілини вважайте абсолютно пружними. Опором руху знехтуйте.
Відповідь запишіть у цілих числах.
Правильна відповідь:
40.0
Кулька вільно скочується похилою площиною $A B$, довжина якої 1 метр. Початкова швидкість кульки дорівнює нулю. Провівши 5 експериментів, учень визначив час, за який кулька проходить відстань $A B: t_{1}=0,993 \mathrm{~с} ; t_{2}=0,995 \mathrm{~с}$; $t_{3}=0,987 \mathrm{~с} ; t_{4}=1,012 \mathrm{~с} ; t_{5}=1,013 \mathrm{~с}$.
Визначте середнє прискорення ($\mathrm{м} / \mathrm{с}^2$) кульки
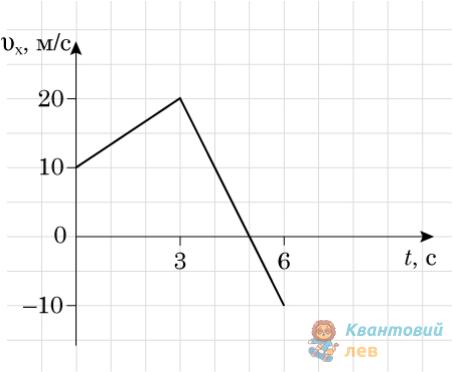
На рисунку зображено графік залежності проекції швидкості $v_{x}$ руху автомобіля від часу $t$.
Визначте модуль переміщення автомобіля за $6\mathrm{~с}$.
Відповідь запишіть у метрах ($\mathrm{м}$).
Правильна відповідь:
60.0