Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
Укажіть із-поміж наведених назву процесу, під час якого середня кінетична енергія хаотичного руху молекул газу сталої маси зростає.
Г
ізобарне розширення
Правильна відповідь
У газі певної маси концентрація молекул залишається сталою, а їхня середня кінетична енергія зростає під час
А
ізохорного нагрівання
Правильна відповідь
Унаслідок нагрівання абсолютна температура ідеального газу в герметично закритій посудині збільшилася від $250 \mathrm{~К}$ до $1000 \mathrm{~К}$. У скільки разів збільшилася кількість зіткнень молекул газу зі стінками посудини за $1 \mathrm{~c}$?
А
у 2 рази
Правильна відповідь
Визначте, під час якого процесу в газі концентрація молекул зростає, а їхня середня кінетична енергія залишається сталою.
Б
ізотермічне стискання
Правильна відповідь
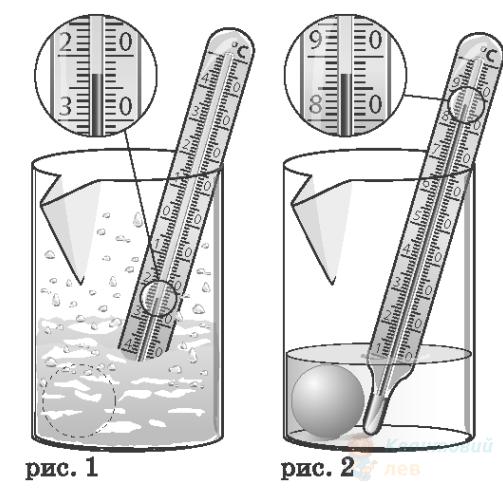
До дна склянки приклеїли герметичну кульку, заповнену гелієм. Після цього склянку з кулькою заповнили снігом (див. рисунок 1). На рисунку 2 зображено ту ж саму склянку після того, як сніг розтанув, а вода, що утворилася, дещо нагрілася. Вимірювання температури проводилися після встановлення теплової рівноваги у склянці. Використовуючи покази термометрів, визначте, у скільки разів збільшилася середня квадратична швидкість молекул гелію у кульці.
А
у 1,2 раза
Правильна відповідь
Температура газу підвищилася від $27^{\circ} \mathrm{C}$ до $90^{\circ} \mathrm{C}$. Визначте, у скільки разів збільшилася середня квадратична швидкість молекул газу.
А
в 1,1 раза
Правильна відповідь
За якою формулою можна визначити середню кінетичну енергію поступального хаотичного руху молекул газу?
А
$\bar{E}_{\mathrm{k}} = \frac{1}{3} \rho \bar{v}^{2}$
Б
$\bar{E}_{\mathrm{k}} = \frac{1}{3} k T$
В
$\bar{E}_{\mathrm{k}} = \frac{2}{3} k T$
Г
$\bar{E}_{\mathrm{k}} = \frac{3}{2} k T$
Правильна відповідь
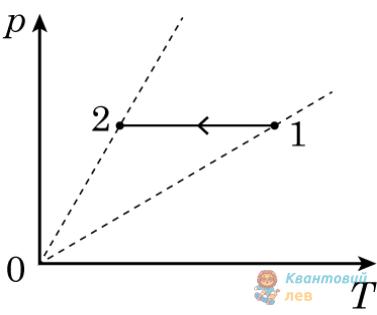
На рисунку зображено графік залежності тиску $\large p$ ідеального газу сталої маси від абсолютної температури $T$.
Як змінились об'єм газу й середня квадратична швидкість руху його молекул під час переходу зі стану 1 у стан 2?
Б
зменшився; зменшилася
Правильна відповідь
Установіть відповідність між назвою фізичної сталої (1-4) та її фізичним змістом (А – Д).
Варіанти зліва
1
стала Авогадро $N_{\mathrm{A}}$
Варіанти справа
А
$2 / 3$ від зміни середньої кінетичної енергії поступального руху молекул за зміни температури на $1 \mathrm{~К}$
Б
кількість атомів (молекул), які містяться в будь-якій речовині кількістю $1 \mathrm{~моль}$
В
сила притягання двох матеріальних точок масою по $1 \mathrm{~кг}$ на відстані $1 \mathrm{~м}$
Г
відношення енергії світлового кванта до частоти світла
Д
відношення маси молекули цієї речовини до $1 / 12$ маси атома Карбону
Установіть відповідність між назвами формул (1-4), що стосуються молекулярно-кінетичної теорії та термодинаміки, та самими формулами (А – Д).
Позначення: $p$ – тиск ідеального газу, $n$ – концентрація молекул газу, $m_{0}$ – маса молекули, $m$ – маса газу, $M$ – молярна маса, $\bar{v}$ – середня швидкість молекули, $k$ – стала Больцмана, $R$ – універсальна газова стала, $T$ – температура, $U$ – внутрішня енергія, $Q$ – кількість теплоти, $A$ – робота, $c$ – питома теплоємність.
Варіанти зліва
1
основне рівняння молекулярно-кінетичної теорії ідеального газу
2
перший закон термодинаміки
3
загальне рівняння стану ідеального газу для довільної його кількості
4
середня кінетична енергія молекул одноатомного газу
Варіанти справа
А
$p=\frac{1}{3} n m_{0} \bar{v}^{2}$
Б
$\bar{E}=\frac{3}{2} k T$
Середня квадратична швидкість атома гелію становить $3000 \mathrm{~м}/\mathrm{с}$. Молярна маса гелію дорівнює $4 \cdot 10^{-5} \mathrm{~кг} / \mathrm{моль}$. Уважайте, що універсальна газова стала дорівнює $8,3 \mathrm{~Дж} / ( \mathrm{моль} \cdot \mathrm{К} )$.
Визначте внутрішню енергію ($\mathrm{кДж}$) газу кількістю 1 моль.
Правильна відповідь:
18.0
Середня квадратична швидкість атома гелію становить $3000 \mathrm{~м}/\mathrm{с}$. Молярна маса гелію дорівнює $4 \cdot 10^{-5} \mathrm{~кг} / \mathrm{моль}$. Уважайте, що універсальна газова стала дорівнює $8,3 \mathrm{~Дж} / ( \mathrm{моль} \cdot \mathrm{К} )$.
Обчисліть температуру газу (у кельвінах).
Правильна відповідь:
1500.0