Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
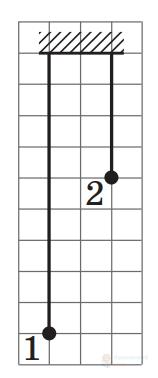
На рисунку схематично зображено математичні маятники 1 і 2. Період малих вільних коливань математичного маятника 1 дорівнює $1,20 \mathrm{~c}$. Визначте період малих вільних коливань математичного маятника 2.
Г
$0,80 \mathrm{~c}$
Правильна відповідь
Тягарець коливається на довгій нерозтяжній нитці. Для того щоб збільшився період малих коливань у 2 рази, треба збільшити
В
довжину нитки в 4 рази
Правильна відповідь
Сталева та дерев'яна суцільні кульки однакового радіуса підвішені на однакових довгих легких нерозтяжних нитках. Їх відводять убік на однакову невелику відстань і відпускають. Яке з наведених тверджень щодо коливань кульок правильне?
А
у сталевої кульки період коливань більший
Б
у дерев'яної кульки період коливань більший
В
у сталевої кульки коливання затухають швидше
Г
у дерев'яної кульки коливання затухають швидше
Правильна відповідь
Мавпочка, яка здійснювала малі коливання у вертикальній площині на ліані довжиною $L$, піднялася по ній на відстань $l$ угору, продовжуючи гойдання. Як унаслідок цього змінився період коливань такого «маятника»? Ліану вважайте нерозтяжною й невагомою. Довжина ліани значно більша за зріст мавпочки.
А
період коливань зменшився пропорційно до $\sqrt{L-l}$
Правильна відповідь
Б
період коливань збільшився пропорційно до $L-l$
В
період коливань не змінився
Г
період коливань збільшився пропорційно до $\sqrt{L-l}$
На легких нерозтяжних нитках однакової довжини підвішено дві маленькі кульки однакового радіуса. Першу кульку виготовлено з деревини, густина якої дорівнює $500 \mathrm{~кг} / \mathrm{м}^{3}$, другу – з металу, густина якого становить $8000 \mathrm{~кг} / \mathrm{м}^{3}$. Порівняйте періоди $T_{1}$ і $T_{2}$ малих коливань відповідних кульок на нитках. Опором повітря знехтуйте.
Б
$T_{1}=T_{2}$
Правильна відповідь
Невелика посудина з водою, у дні якої є маленький отвір, коливається на дуже довгій легкій нерозтяжній мотузці. Початковий період коливань дорівнює $6 \mathrm{~c}$. Вода потроху витікає. Визначте період коливань, коли маса посудини з водою зменшиться в 3 рази. Масою порожньої посудини знехтуйте.
Б
$6 \mathrm{~c}$
Правильна відповідь
Маятник, який можна вважати математичним, здійснив за певний інтервал часу 100 коливань. Довжину нитки маятника збільшили у 4 рази. Визначте кількість коливань маятника за такий же інтервал часу.
Маятник, який можна вважати математичним, здійснив за певний інтервал часу 100 коливань. Довжину нитки маятника зменшили в 4 рази. Визначте кількість коливань маятника за такий же інтервал часу.
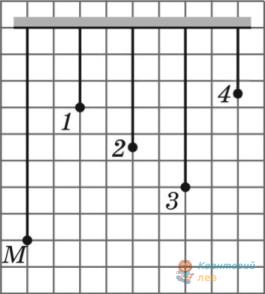
На рисунку зображено нитяні маятники, які можна вважати математичними. Період малих вільних коливань маятника $M$ дорівнює $1,6 \mathrm{~с}$. Позначте маятник, період малих вільних коливань якого дорівнює $1,2 \mathrm{~с}$. Вважайте, що відстані між лініями сітки рівні.
Б
маятник 2
Правильна відповідь
Установіть відповідність між процесом (1-4) та формулою (А – Д), що його описує.
Позначення: $T$ – період коливань, $l, l_{1}, l_{2}$ – довжини, $g$ – прискорення вільного падіння, $F, F_{1}, F_{2}$ – сили, $m, m_{1}, m_{2}$ – маси, $k$ – жорсткість, $v_{1}, v_{2}, u_{1}$, $u_{2}$ – швидкості, $G$ – гравітаційна стала, $R$ – відстань.
Варіанти зліва
1
гайка здійснює малі коливання на нитці
2
гайку закручують гайковим ключем
3
дві кульки пружно зіткнулися
4
тіло коливається на пружині
Варіанти справа
А
$T=2 \pi \sqrt{\frac{l}{g}}$
Б
$F_{1} l_{1}=F_{2} l_{2}$
В
$T=2 \pi \sqrt{\frac{m}{k}}$
Г
$m_{1} \vec{v}_{1}+m_{2} \vec{v}_{2}=m_{1} \vec{u}_{1}+m_{2} \vec{u}_{2}$
Д
$F=G \frac{m_{1} m_{2}}{R^{2}}$
Установіть відповідність між процесом (1-4) та формулою (А-Д), що його описує.
Варіанти зліва
1
взаємодіють Венера і Марс
2
розтягується гумова нитка
3
стрічка транспортера пересуває цеглину, яка лежить на ній
4
маленька сталева кулька коливається на довгій нерозтяжній нитці
Варіанти справа
А
$F=G \frac{m_{1} \cdot m_{2}}{R^{2}}$
Б
$T=2 \pi \sqrt{\frac{l}{g}}$
Тягарець масою $m$, підвішений на довгій нитці, здійснює малі коливання з амплітудою $A$. Установіть відповідність між фізичною величиною (1-4), що характеризує коливальний рух, та характером залежності (А – Д) величини від $m$ і $A$.
Варіанти зліва
3
максимальна висота тягарця над нижньою точкою його траєкторії
4
максимальна швидкість тягарця
Варіанти справа
А
величина пропорційна $m$ і $A^{2}$
Б
величина пропорційна $m$ і $A$
В
величина не залежить від $m$ і $A$
Г
величина пропорційна $A$, не залежить від $m$
Д
величина пропорційна $A^{2}$, не залежить від $m$
Установіть відповідність між фізичними величинами та математичними виразами, що їх описують.
Варіанти зліва
1
потенціальна енергія тіла, що здійснює горизонтальні коливання на пружині
2
період коливань математичного маятника
3
кінетична енергія тіла, що здійснює коливання
4
період коливань тіла, що здійснює коливання на пружині
Варіанти справа
Б
$2 \pi \sqrt{\frac{m}{k}}$
В
$A \sin(\omega t+\varphi_{0})$
Д
$2 \pi \sqrt{\frac{l}{g}}$
Установіть відповідність між назвами формул, що стосуються коливань, та власне самими формулами.
Варіанти зліва
1
період коливань тіла, що здійснює коливання на пружині;
2
рівняння гармонічних коливань;
3
потенціальна енергія пружини, на якій тіло здійснює горизонтальні коливання;
4
період коливань математичного маятника.
Варіанти справа
А
$E_{\mathrm{k}}=\frac{m v^{2}}{2}$;
Б
$T=2 \pi \sqrt{\frac{l}{g}}$;
В
$E_{\mathrm{p}}=\frac{k x^{2}}{2}$;
Г
$x_{1}=A \cos \left(\omega \mathrm{t}+\varphi_{0}\right), x_{2}=A \sin \left(\omega \mathrm{t}+\varphi_{0}\right)$;
Д
$T=2 \pi \sqrt{\frac{m}{k}}$.
Довжина дитячої гойдалки становить $1,6 \mathrm{~м}$. З яким інтервалом часу її потрібно підштовхувати з однієї сторони, щоби гойдалка сильніше розгойдувалася? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у секундах ($\mathrm{с}$) і округліть до десятих.
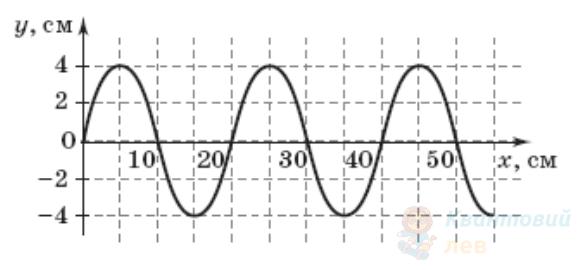
Маятник з дуже легким маркером на кінці закріплено на рухомому іграшковому автомобілі. Маятник коливається в площині $z O y$, перпендикулярній напрямку руху автомобіля. Довжина маятника дорівнює $0,1 \mathrm{~м}$. Маркер залишив на столі слід, зображений на рисунку. Визначте швидкість автомобіля (у м/с). Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}, \pi=3,14$. Відповідь округліть до сотих.
Правильна відповідь:
0.32
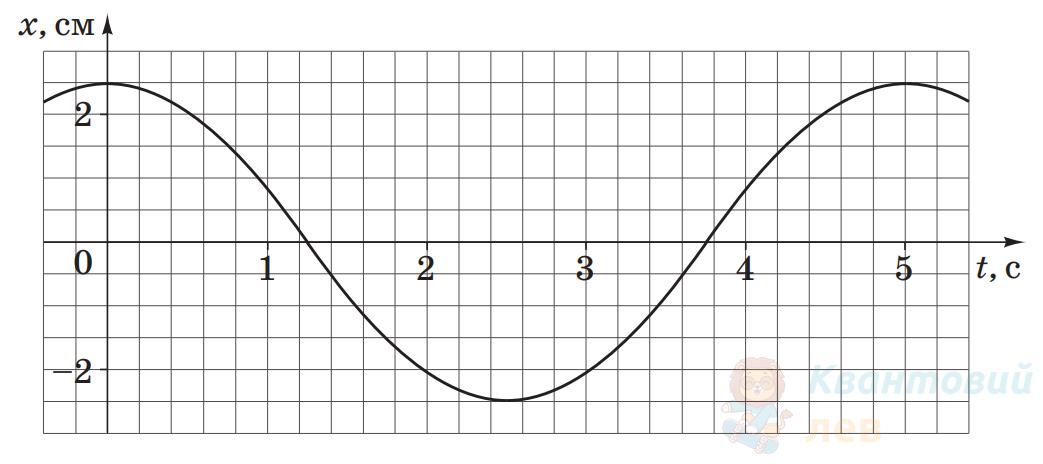
На рисунку зображено графік коливань математичного маятника. Визначте довжину математичного маятника. Уважайте, що $\pi^{2}=g$. Відповідь запишіть у метрах.
Правильна відповідь:
6.25
Математичний маятник відхилили від положення рівноваги на кут, що дорівнює 0,1 радіана, й відпустили. Який шлях пройде важок маятника за $5,5 \mathrm{~c}$? Довжина маятника дорівнює $1 \mathrm{~м}$. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}, \pi^{2}=10$.
Відповідь запишіть у метрах.