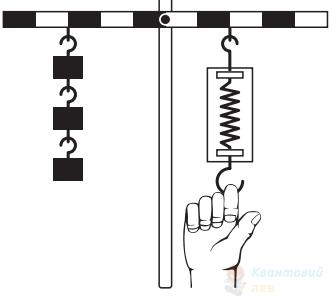
На важелі, що може вільно обертатися навколо осі O, підвішено кілька однакових тягарців (див. фото). Визначте точку, у якій необхідно підвісити ще один такий самий тягарець, щоб важіль зрівноважився й зайняв горизонтальне положення. Уважайте, що спочатку важіль без тягарців був зрівноважений.

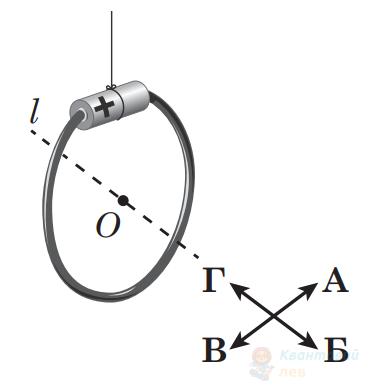
Турист виготовив із підручних матеріалів електромагнітний компас. Для цього він з'єднав полюси гальванічного елемента дротиною так, що утворився круглий виток (на рисунку $l$ – вісь, яка проходить через центр витка $O$ перпендикулярно до його площини). Отриману конструкцію турист підвісив на нитку. Через деякий час вона припинила рухатися і встановилася так, як показано на рисунку. Визначте, у якому напрямку (А – Г) північ – одна із чотирьох головних сторін горизонту.

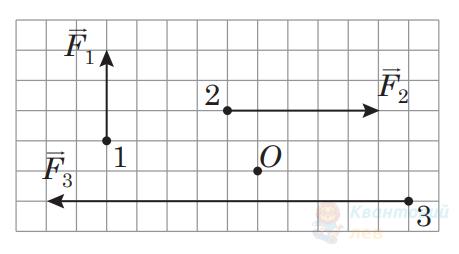
До точок $1,2,3$ в площині прямокутної пластини прикладено сили $F_{1}=3 \mathrm{H}, F_{2}=5 \mathrm{H}$, $F_{3}=12 \mathrm{H}$ відповідно (див. рисунок). Укажіть правильне співвідношення модулів моментів цих сил $M_{1}, M_{2}, M_{3}$ відносно осі, що проходить перпендикулярно до площини пластини через точку $O$.

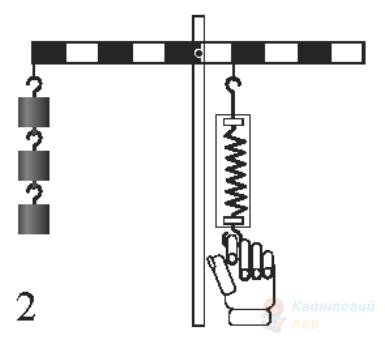
Важіль, зображений на рисунку, перебуває в рівновазі. Маса кожного тягарця становить $100 \mathrm{~г}$. Визначте показ динамометра. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.

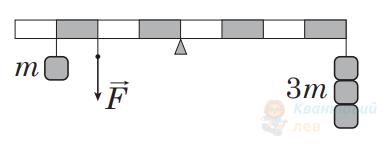
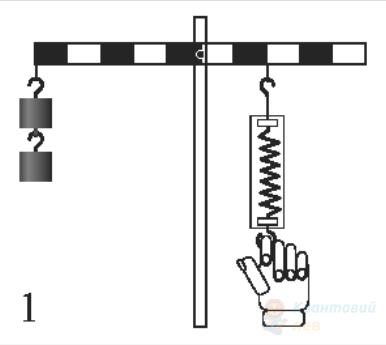
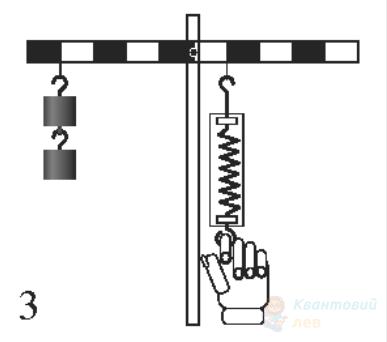
На рисунку зображено важіль, до якого підвішено тягарці масою ( $m$ ) $100 \mathrm{~г}$ кожний. Якою є сила натягу нитки $\vec{F}$, якщо важіль перебуває в рівновазі? Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.

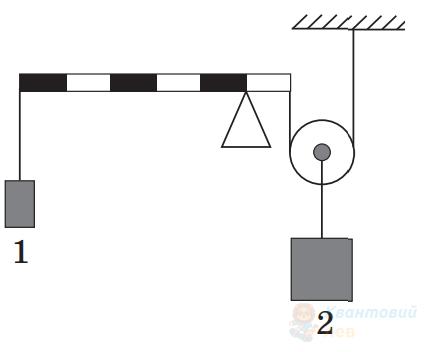
Точка опори ділить важіль у співвідношенні $1:5$. Якою є маса вантажу 2, якщо важіль перебуває в рівновазі? Маса вантажу 1 становить $30 \mathrm{~кг}$. Масами блока та важеля, а також тертям у блоці знехтуйте.

Важіль (1) без тертя може вільно обертатися навколо осі (2). Спочатку за відсутності важків та вантажу (3) важіль було зрівноважено. Визначте масу вантажу (3).

Визначте, яку загальну масу має смугастий циліндричний вантаж. Призматичні вантажі на фото мають масу по $100 \mathrm{~г}$ кожен.

На коротке плече важеля довжиною $16 \mathrm{~см}$ діє сила $100 \mathrm{~Н}$. Щоб підняти вантаж, до довгого плеча довжиною $80 \mathrm{~см}$ було прикладено силу $25 \mathrm{~Н}$. Визначте ККД важеля.

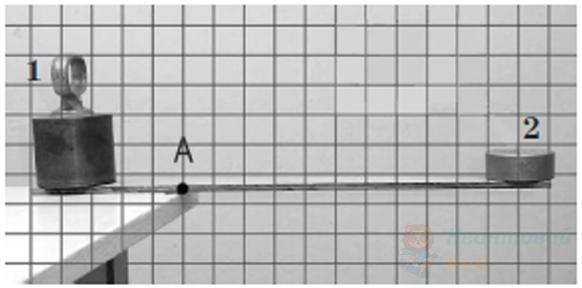
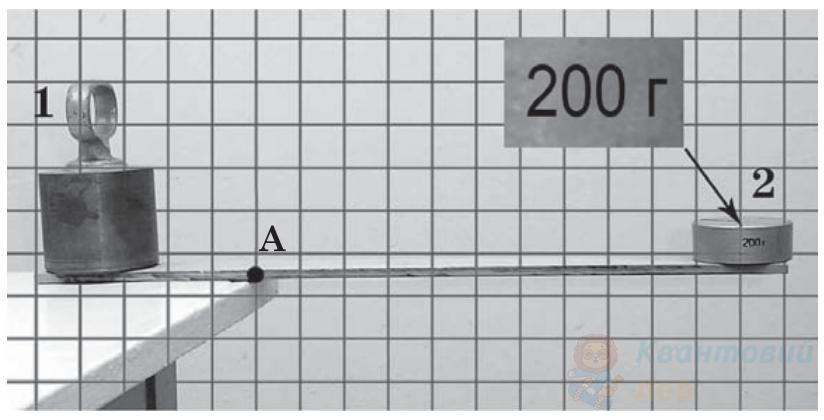
Обчисліть момент сили тяжіння, яка діє на вантаж 2, відносно горизонтальної осі, що проходить через точку $A$. Масою дерев'яної рейки знехтуйте. Період сітки, накладеної на фото, дорівнює $5 \mathrm{~см}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.

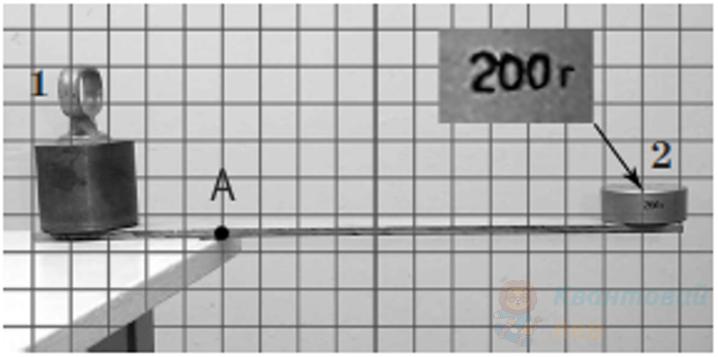
Обчисліть масу вантажу 2, якщо момент сили тяжіння цього вантажу відносно горизонтальної осі, що проходить через точку $A$ дорівнює $0,55 \mathrm{~H} \cdot \mathrm{м}$. Масою дерев'яної рейки знехтуйте. Період сітки, накладеної на фото, дорівнює $2,5 \mathrm{~см}$. Вважайте, що $g = 10 \mathrm{~м} / \mathrm{с}^{2}$.

Установіть відповідність між процесом (1-4) та формулою (А – Д), що його описує.

Позначення: $T$ – період коливань, $l, l_{1}, l_{2}$ – довжини, $g$ – прискорення вільного падіння, $F, F_{1}, F_{2}$ – сили, $m, m_{1}, m_{2}$ – маси, $k$ – жорсткість, $v_{1}, v_{2}, u_{1}$, $u_{2}$ – швидкості, $G$ – гравітаційна стала, $R$ – відстань.

Установіть відповідність між процесом (1-4) та формулою (А-Д), що його описує.

Установіть відповідність між процесами та формулами, що їх описують.

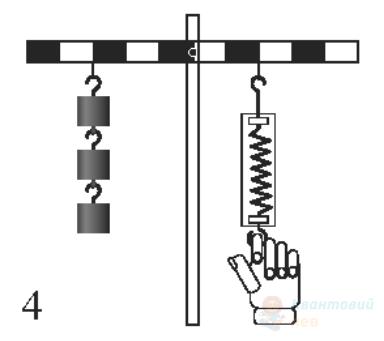
Важелі, зображені на рисунках, знаходяться у рівновазі. Кожен тягарець має масу $100 \mathrm{~г}$. Установіть відповідність між цими рисунками і показами динамометрів. Вважайте, що $g=10 \mathrm{~м} / \mathrm{с}^{2}$

Якщо вантаж $t$ невідомої маси підвісити до короткого плеча важеля, то його можна зрівноважити вантажем масою $400 \mathrm{~г}$. Якщо вантаж $t$ підвісити до довгого плеча важеля, не змінюючи положення точки опори $O$, то його можна зрівноважити вантажем масою $900 \mathrm{~г}$. Масою важеля знехтуйте.

Визначте відношення довжини більшого плеча важеля до меншого.

Якщо вантаж $t$ невідомої маси підвісити до короткого плеча важеля, то його можна зрівноважити вантажем масою $400 \mathrm{~г}$. Якщо вантаж $t$ підвісити до довгого плеча важеля, не змінюючи положення точки опори $O$, то його можна зрівноважити вантажем масою $900 \mathrm{~г}$. Масою важеля знехтуйте.

Яка маса $m$ вантажу?
Відповідь запишіть у грамах ($\mathrm{г}$)

Визначте модуль моменту сили тяжіння, яка діє на вантаж 2, відносно горизонтальної осі, що проходить через точку А перпендикулярно до рейки. Період сітки, накладеної на фото, дорівнює $5 \mathrm{~см}$. Уважайте, що прискорення вільного падіння дорівнює $10 \mathrm{~м} / \mathrm{с}^{2}$.
Відповідь запишіть у ньютон-метрах ($\mathrm{Н} \cdot \mathrm{м}$)

На схематичному рисунку зображено однорідний легкий стержень $A B$ завдовжки $40 \mathrm{~см}$, до обох кінців якого підвішено важки. Визначте, на якій відстані від лівого кінця стержня ($A$) потрібно поставити опору, щоб він перебував у рівновазі.
Відповідь запишіть у сантиметрах ($\mathrm{см}$)

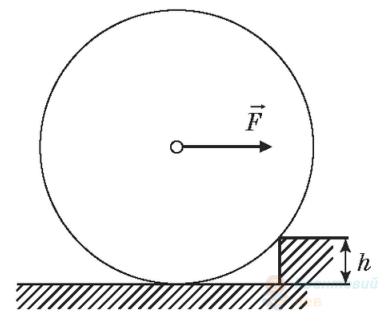
Визначте модуль мінімальної, горизонтально напрямленої сили $\vec{F}$, яку потрібно прикласти до циліндричного котка радіусом $5 \mathrm{~см}$, щоб підняти його на сходинку висотою $h = 1$ см. Вага котка дорівнює $4 \mathrm{~Н}$ . Відповідь запишіть у ньютонах.

Важіль 1 без тертя може вільно обертатися навколо осі 2, як зображено на рисунку. Спочатку без важків та вантажу 3 важіль було зрівноважено. Визначте масу вантажу 3.
Відповідь запишіть у кілограмах ($\mathrm{кг}$).