Скачати цей тест
Всі тести у форматі PDF, презентації та Word документи для підготовки та викладання
Дізнатися більше
У калориметр із водою, маса якої $1 \mathrm{~кг}$, а температура $20^{\circ} \mathrm{C}$, поклали лід масою $1 \mathrm{~кг}$ за температури $-30^{\circ} \mathrm{C}$. Уважайте, що питома теплоємність води дорівнює $4200 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$, питома теплоємність льоду $2100 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$, питома теплота плавлення льоду становить $330 \mathrm{~кДж} / \mathrm{кг} $, температура плавлення льоду $0{ }^{\circ} \mathrm{C}$. Теплоємність калориметра та теплообмін із навколишнім середовищем не враховуйте. Після встановлення теплової рівноваги в калориметрі
Б
частина льоду розтане
Правильна відповідь
Визначте масу палива з питомою теплотою згоряння $34 \mathrm{~МДж} / \mathrm{кг}$, яка потрібна, щоб розтопити лід масою $2 \mathrm{~кг}$ за початкової температури $0{ }^{\circ} \mathrm{C}$. Питома теплота плавлення льоду становить $340 \mathrm{~кДж} / \mathrm{кг}$.
Б
$20 \mathrm{~г}$
Правильна відповідь
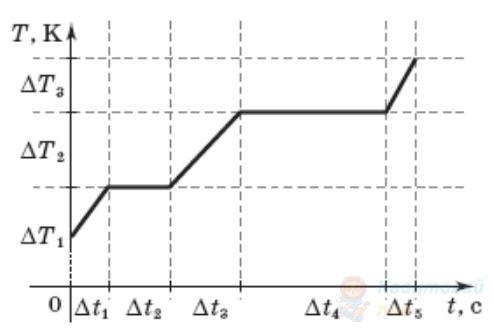
На рисунку зображено графік залежності абсолютної температури $T$ води масою $m$ від часу $t$ при здійсненні теплопередачі з постійною потужністю $P$. У момент часу $t=0$ с вода була у твердому стані. За допомогою якого із зазначених виразів можна визначити питому теплоємність води в рідкому стані за результатами цього досліду?
А
$\frac{P \Delta t_{1}}{m \Delta T_{2}}$
Б
$\frac{P \Delta t_{2}}{m}$
В
$\frac{P \Delta t_{2}}{m \Delta T_{2}}$
Правильна відповідь
Г
$\frac{P \Delta t_{4}}{m}$
На скільки зміниться внутрішня енергія льоду масою $3 \mathrm{~кг}$ у процесі його танення за нормальних умов (тиск $p_{\text{п}}$ дорівнює $101 \mathrm{~кПа}$, температура $T$ становить $273 \mathrm{~К}$); питома теплота плавлення льоду дорівнює $3,3 \cdot 10^{5} \mathrm{~Дж} / \mathrm{кг}$.
А
зменшиться на $9,9 \cdot 10^{5} \mathrm{~Дж}$
Б
зменшиться на $3,3 \cdot 10^{5} \mathrm{~Дж}$
В
збільшиться на $9,9 \cdot 10^{5} \mathrm{~Дж}$
Правильна відповідь
Г
збільшиться на $3,3 \cdot 10^{5} \mathrm{~Дж}$
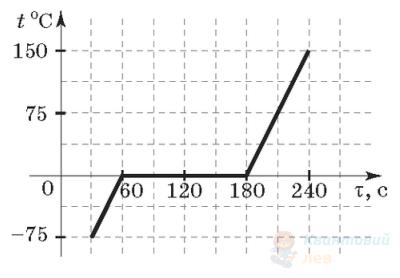
На рисунку зображено графік залежності температури речовини $t$, що знаходиться в калориметрі, від часу $\tau$. У початковий момент часу речовина була в твердому стані. Вважайте, що теплоємність калориметра і втрати тепла є нехтовно малими, а речовині в калориметрі щосекунди передається одна й та сама кількість теплоти. Визначте питому теплоємність речовини в рідкому стані. Питома теплота плавлення речовини дорівнює $60 \mathrm{~кДж} / \mathrm{кг}$.
А
$200 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$
Правильна відповідь
Б
$300 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$
В
$400 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$
Г
$600 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$
Установіть відповідність між назвою фізичної величини і математичним виразом, за яким її можна визначити.
Варіанти зліва
1
кількість теплоти, необхідна для нагрівання тіла
2
питома теплота плавлення кристалічної речовини
3
кількість теплоти, що виділяється при згорянні палива
4
коефіцієнт корисної дії ідеальної теплової машини
Варіанти справа
В
$\frac{Q}{m \cdot \Delta T}$
Д
$1 - \frac{T_{х}}{T_{н}}$
Установіть відповідність між назвою фізичної величини і математичним виразом, за яким її можна визначити.
Варіанти зліва
1
питома теплоємність речовини
2
питома теплота плавлення кристалічної речовини
3
зміна внутрішньої енергії при зміні температури тіла способом теплопередачі
4
коефіцієнт корисної дії реальної теплової машини
Варіанти справа
В
$\frac{Q}{m \cdot \Delta T}$
Д
$1-\frac{Q_{\mathrm{X}}}{Q_{\mathrm{H}}}$
Нагріту монету поклали на лід, у який вона повністю занурилася. Визначте, за якої мінімальної температури монети це могло відбутися. Температура льоду до того, як на нього поклали монету, становила $0^{\circ} \mathrm{C}$. Густина сплаву, з якого виготовлено монету, дорівнює $9,0 \mathrm{~г} / \mathrm{см}^{3}$, його питома теплоємність $220 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$. Густина льоду становить $900 \mathrm{~кг} / \mathrm{м}^{3}$, питома теплота плавлення льоду – $330 \mathrm{~кДж} / \mathrm{кг}$. Втрати тепла не враховуйте.
Відповідь запишіть у градусах Цельсія ($^{\circ} \mathrm{C}$)
Правильна відповідь:
150.0
У посудині знаходиться колотий лід масою $2 \mathrm{~кг}$, його температура становить $-10{ }^{\circ} \mathrm{C}$. Обчисліть масу води, температура якої $+20^{\circ} \mathrm{C}$, яку потрібно долити в посудину, щоб увесь лід розтанув. Теплоємністю посудини і тепловим обміном із навколишнім середовищем знехтуйте. У відповіді запишіть найменшу необхідну масу ($\mathrm{кг}$) води. Уважайте, що питома теплоємність льоду $2100 \mathrm{~Дж} / (\mathrm{кг} \cdot \mathrm{К})$, води – $4200 \mathrm{~Дж} / (\mathrm{кг} \cdot \mathrm{К})$, а питома теплота плавлення льоду дорівнює $336 \mathrm{~кДж} / \mathrm{кг}$.
Ідеальна теплова машина має як нагрівник резервуар з водою, що кипить ($373 \mathrm{~К}$), а холодильником – ємність з льодом, що тане ($273 \mathrm{~К}$). Яка маса цього льоду розтане у результаті виконання машиною корисної роботи $110 \mathrm{~кДж}$, якщо питома теплота плавлення льоду дорівнює $330 \mathrm{~кДж} / \mathrm{кг}$? Відповідь запишіть у грамах.
Правильна відповідь:
910.0
У металеву посудину, маса якої $200 \mathrm{~г}$, влили $150 \mathrm{~г}$ води і опустили шматок льоду, що мав температуру $0^{\circ} \mathrm{C}$. Початкова температура посудини з водою $25^{\circ} \mathrm{C}$. У момент часу, коли настала теплова рівновага, температура води в металевій посудині стала дорівнювати $5^{\circ} \mathrm{C}$. Визначте масу льоду (у кілограмах). Питома теплоємність металу, з якого виготовлено посудину, дорівнює $410 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$, питома теплоємність води становить $4200 \mathrm{~Дж} / ( \mathrm{кг} \cdot \mathrm{К} )$, питома теплота плавлення льоду дорівнює $3,35 \cdot 10^{5} \mathrm{~Дж} / \mathrm{кг}$. Втратами тепла металевою посудиною з водою знехтуйте.
Правильна відповідь:
0.04